Chương 8: Đại số quan hệ và phép toán quan hệ

Nội dung bài viết

---

Đại số quan hệ rất quan trọng vì nhiều lý do. Đầu tiên, nó cung cấp một nền tảng chính thức cho các hoạt động của mô hình quan hệ. Thứ hai, và có lẽ quan trọng hơn, nó được sử dụng làm cơ sở để triển khai và tối ưu hóa các truy vấn trong các mô-đun xử lý và tối ưu hóa truy vấn, là những phần không thể thiếu của các hệ thống quản lý cơ sở dữ liệu quan hệ (RDBMS), như chúng ta sẽ thảo luận trong Chương 18 và 19. Thứ ba, một số khái niệm của nó được tích hợp vào ngôn ngữ truy vấn chuẩn SQL cho RDBMS. Mặc dù hầu hết các RDBMS thương mại đang sử dụng hiện nay không cung cấp giao diện người dùng cho các truy vấn đại số quan hệ, các hoạt động và chức năng cốt lõi trong các mô-đun bên trong của hầu hết các hệ thống quan hệ đều dựa trên các hoạt động đại số quan hệ. Chúng ta sẽ định nghĩa chi tiết các thao tác này trong Phần 8.1 đến 8.4 của chương này

Trong khi đại số quan hệ định nghĩa một tập hợp các phép toán cho mô hình quan hệ, thì phép tính quan hệ cung cấp một ngôn ngữ khai báo cấp cao hơn để chỉ định các truy vấn quan hệ. Trong một biểu thức tính toán quan hệ, không có thứ tự các thao tác để xác định cách truy xuất kết quả truy vấn—chỉ có thông tin mà kết quả sẽ chứa. Đây là đặc điểm phân biệt chính giữa đại số quan hệ và phép tính quan hệ. Phép tính quan hệ rất quan trọng vì nó có cơ sở vững chắc trong logic toán học và vì ngôn ngữ truy vấn chuẩn (SQL) cho RDBMS có một số nền tảng của nó trong nhiều phép tính quan hệ được gọi là phép tính quan hệ bộ

Đại số quan hệ thường được coi là một phần không thể thiếu của mô hình dữ liệu quan hệ. Hoạt động của nó có thể được chia thành hai nhóm. Một nhóm bao gồm các hoạt động tập hợp từ lý thuyết tập hợp toán học; những điều này có thể áp dụng được vì mỗi mối quan hệ được định nghĩa là một tập hợp các bộ trong mô hình quan hệ chính thức (xem Phần 5.1). Các hoạt động tập hợp bao gồm UNION, INTERSECTION, SET DIFFERENCE và CARTESIAN PRODUCT (còn được gọi là SẢN PHẨM CHÉO). Nhóm còn lại bao gồm các thao tác được phát triển riêng cho cơ sở dữ liệu quan hệ—các thao tác này bao gồm SELECT, PROJECT và JOIN, trong số các thao tác khác. Đầu tiên, chúng ta mô tả các phép toán SELECT và PROJECT trong Phần 8.1 vì chúng là các phép toán đơn nguyên hoạt động trên các quan hệ đơn lẻ. Sau đó, chúng ta thảo luận về các phép toán tập hợp trong Phần 8.2. Trong Phần 8.3, chúng ta thảo luận về JOIN và các phép toán nhị phân phức tạp khác, hoạt động trên hai bảng bằng cách kết hợp các bộ (bản ghi) có liên quan dựa trên các điều kiện nối. Cơ sở dữ liệu quan hệ COMPANY được hiển thị trong Hình 5.6 được sử dụng cho các ví dụ của chúng tôi

1. Các phép toán quan hệ cơ bản SELECT và PROJECT

1.1 Phép chọn (Select)

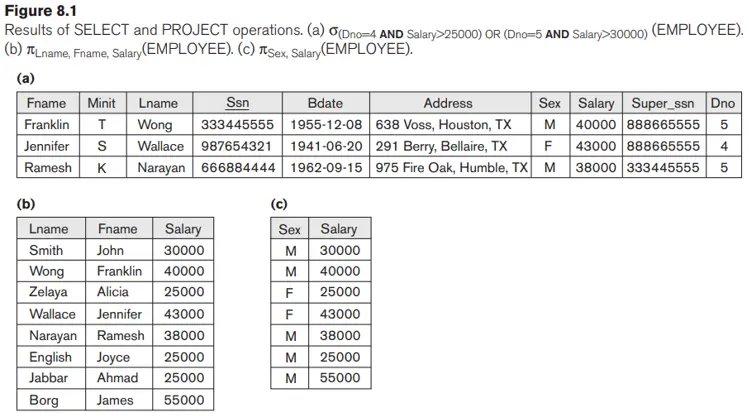
Thao tác SELECT được sử dụng để chọn một tập hợp con của các bộ từ một quan hệ thỏa mãn một điều kiện lựa chọn. Chúng ta có thể coi thao tác CHỌN là một bộ lọc chỉ giữ lại những bộ dữ liệu thỏa mãn điều kiện đủ điều kiện. Ngoài ra, chúng ta có thể xem xét thao tác SELECT để hạn chế các bộ trong mối quan hệ chỉ với những bộ thỏa mãn điều kiện. Thao tác SELECT cũng có thể được hình dung dưới dạng một phân hoạch ngang của quan hệ thành hai tập hợp các bộ dữ liệu – những bộ thỏa mãn điều kiện và được chọn, còn những bộ không thỏa mãn điều kiện và bị lọc ra. Ví dụ: để chọn các bộ EMPLOYEE có bộ phận là 4 hoặc những bộ có mức lương lớn hơn $30.000, chúng ta có thể chỉ định riêng từng bộ trong hai điều kiện này bằng thao tác SELECT như sau:

σDno=4(EMPLOYEE)

σSalary>30000(EMPLOYEE)

Nhìn chung, thao tác SELECT được ký hiệu là

σ_{<slection condition>}(R)

trong đó ký hiệu σ (sigma) được sử dụng để biểu thị toán tử SELECT  và điều kiện lựa chọn là một biểu thức Boolean (điều kiện) được xác định trên các thuộc tính của quan hệ R. Lưu ý rằng R nói chung là một biểu thức đại số quan hệ có kết quả là một quan hệ—đơn giản nhất biểu thức như vậy chỉ là tên của một quan hệ cơ sở dữ liệu. Mối quan hệ kết quả từ thao tác SELECT có cùng thuộc tính với R

Biểu thức Boolean được chỉ định trong <slection condition> được tạo thành từ một số mệnh đề có dạng

<attribute name><comparision op><constant value>

Hoặc

<attribute name><comparision op><constant value>

Trong đó <attribute name> là tên của một thuộc tính của R, <comparision op> là một trong các toán tử {=,≥, ≠}, và <constant value> là một giá trị không đổi từ miền thuộc tính. Các mệnh đề có thể được kết nối bởi các toán tử Boolean tiêu chuẩn AND, OR, và không tạo thành một điều kiện lựa chọn chung. Ví dụ: để chọn các bộ dữ liệu cho tất cả nhân viên làm việc ở bộ phận 4 và kiếm được hơn 25.000 đô la mỗi năm hoặc làm việc ở bộ phận 5 và kiếm được hơn 30.000 đô la, chúng ta có thể chỉ định thao tác SELECT sau:

σ_{(Dno=4 AND Salary>25000) OR (Dno=5 AND Salary>30000)}(EMPLOYEE)

Kết quả được thể hiện trong hình 8.1(a)

Lưu ý rằng tất cả các toán tử so sánh trong tập hợp {=, , ≥, ≠} có thể áp dụng cho các thuộc tính có miền giá trị được sắp xếp, chẳng hạn như miền số hoặc ngày. Miền của các chuỗi ký tự cũng được coi là được sắp xếp dựa trên trình tự đối chiếu của các ký tự. Nếu miền của một thuộc tính là một tập hợp các giá trị không có thứ tự, thì chỉ có thể sử dụng các toán tử so sánh trong tập hợp {=, ≠}. Một ví dụ về miền không có thứ tự là miền Màu = { 'đỏ', 'xanh lam', 'xanh lục', 'trắng', 'vàng', …}, trong đó không có thứ tự nào được chỉ định giữa các màu khác nhau. Một số miền cho phép bổ sung các loại toán tử so sánh; ví dụ: một miền chuỗi ký tự có thể cho phép toán tử so sánh SUBSTRING_OF

Nhìn chung, kết quả của thao tác SELECT có thể được xác định như sau. <selection condittion> được áp dụng độc lập cho từng bộ riêng lẻ t trong R. Điều này được thực hiện bằng cách thay thế mỗi lần xuất hiện của một thuộc tính Ai trong điều kiện lựa chọn bằng giá trị của nó trong bộ t[Ai]. Nếu điều kiện đánh giá là TRUE, thì bộ t được chọn. Tất cả các bộ đã chọn xuất hiện trong kết quả của thao tác SELECT. Các điều kiện Boolean AND, OR và NOT có cách hiểu thông thường như sau:

• (cond1 AND cond2) là TRUE nếu cả (cond1) và (cond2) đều TRUE; mặt khác, đó là FALSE.
• (cond1 OR cond2) là TRUE nếu (cond1) hoặc (cond2) hoặc cả hai đều TRUE; nếu không, nó là FALSE.
• (KHÔNG cond) là TRUE nếu cond là FALSE; nếu không, nó là FALSE

Toán tử SELECT là đơn nguyên; nghĩa là, nó được áp dụng cho một quan hệ duy nhất. Hơn nữa, thao tác chọn được áp dụng cho từng bộ riêng lẻ; do đó, các điều kiện lựa chọn không thể bao gồm nhiều hơn một bộ. Bậc của quan hệ do thao tác SELECT tạo ra—số thuộc tính của nó—bằng với bậc của R. Số bộ trong quan hệ kết quả luôn nhỏ hơn hoặc bằng số bộ trong R. Nghĩa là, |σc (R)| ≤ |R| đối với bất kỳ điều kiện nào. Tỷ lệ bộ dữ liệu được chọn bởi một điều kiện lựa chọn được gọi là độ chọn lọc của điều kiện.

Lưu ý rằng phép toán SELECT có tính chất giao hoán; đó là

σ_<cond2>(σ_<cond1> (R)) = σ_<cond1>(σ_<cond2>(R))

Do đó, một chuỗi các SELECT có thể được áp dụng theo bất kỳ thứ tự nào. Ngoài ra, chúng ta luôn có thể kết hợp một loạt (hoặc chuỗi) các thao tác SELECT thành một thao tác SELECT duy nhất với điều kiện liên kết (AND); đó là

σ_<cond1>(σ_<cond2>(... (σ_<condn>(R)) ...)) = σ_{<cond2>AND<cond1>AND<condn>}(R)

Trong SQL, điều kiện SELECT thường được chỉ định trong mệnh đề WHERE của truy vấn. Ví dụ, hoạt động sau đây:

σ_{Dno=4 AND Salary>25000} (EMPLOYEE)

Được thể hiện bằng câu lệnh sau:

SELECT *

FROM EMPLOYEE

WHERE Dno=4 AND Salary>25000;

1.2 Phép chiếu (PROJECT)

Nếu chúng ta coi một quan hệ là một bảng, thì thao tác SELECT sẽ chọn một số hàng từ bảng trong khi loại bỏ các hàng khác. Mặt khác, thao tác PROJECT chọn một số cột nhất định từ bảng và loại bỏ các cột khác. Nếu chúng ta chỉ quan tâm đến một số thuộc tính nhất định của một quan hệ, thì chúng ta sử dụng phép toán PROJECT để chỉ chiếu quan hệ lên các thuộc tính này. Do đó, kết quả của thao tác PROJECT có thể được hình dung dưới dạng phân vùng theo chiều dọc của mối quan hệ thành hai mối quan hệ:

Một gồm có các cột (thuộc tính) cần thiết và chứa kết quả của thao tác, còn cột kia chứa các cột bị loại bỏ. Ví dụ, để liệt kê họ và tên cũng như mức lương của từng nhân viên, chúng ta có thể sử dụng thao tác PROJECT như sau:

π_{Lname, Fname, Salary}(EMPLOYEE)

Mối quan hệ kết quả được thể hiện trong Hình 8.1(b). Ký hiệu chung của phép chiếu là

π_{<attribute list>}(R)

trong đó π (pi) là ký hiệu được sử dụng để biểu diễn phép toán DỰ ÁN và <attribute list> là danh sách con mong muốn của các thuộc tính từ các thuộc tính của quan hệ R. Một lần nữa, lưu ý rằng R nói chung là một biểu thức đại số quan hệ có kết quả là một quan hệ, trong trường hợp đơn giản nhất chỉ là tên của một quan hệ cơ sở dữ liệu. Kết quả của thao tác PROJECT (phép chiếu) chỉ có các thuộc tính được chỉ định trong <attribute list> theo thứ tự như chúng xuất hiện trong danh sách. Do đó, bậc của nó bằng với số thuộc tính trong <attribute list>.

Nếu danh sách thuộc tính chỉ bao gồm các thuộc tính không khóa của R, thì các bộ dữ liệu trùng lặp có khả năng xảy ra. Phép toán PROJECT loại bỏ bất kỳ bộ dữ liệu trùng lặp nào, do đó, kết quả của phép toán PROJECT là một tập hợp các bộ dữ liệu riêng biệt và do đó là một quan hệ hợp lệ. Điều này được gọi là loại bỏ trùng lặp. Ví dụ: xem xét hoạt động PROJECT sau:

π_{Sex, Salary}(EMPLOYEE)

Kết quả được thể hiện trong Hình 8.1(c). Lưu ý rằng bộ giá trị chỉ xuất hiện một lần trong Hình 8.1(c), mặc dù tổ hợp các giá trị này xuất hiện hai lần trong quan hệ EMPLOYEE. Loại bỏ trùng lặp bao gồm sắp xếp hoặc một số kỹ thuật khác để phát hiện các bản sao và do đó bổ sung thêm quá trình xử lý. Nếu trùng lặp không được loại bỏ, kết quả sẽ là nhiều bộ hoặc một túi các bộ chứ không phải là một bộ. Điều này không được phép trong mô hình quan hệ chính thức nhưng được phép trong SQL

Số lượng các bộ trong một quan hệ do phép toán PROJECT tạo ra luôn nhỏ hơn hoặc bằng số lượng các bộ trong R. Nếu danh sách phép chiếu là một siêu khóa của R—nghĩa là nó bao gồm một số khóa của R—thì quan hệ kết quả có cùng số lượng bộ dữ liệu như R. Hơn nữa, miễn là <list2> chứa các thuộc tính trong <list1>; mặt khác, phía bên tay trái là một biểu thức không chính xác. Cũng cần lưu ý rằng tính giao hoán không tồn tại trên PROJECT.

π_<list1> (π_<list2>(R)) = π_<list1>(R)

Trong SQL, danh sách thuộc tính PROJECT được chỉ định trong mệnh đề SELECT của truy vấn. Ví dụ, hoạt động sau đây:

π_{Sex, Salary}(EMPLOYEE)

sẽ tương ứng với truy vấn SQL sau:

SELECT DISTINCT Sex, Salary

FROM EMPLOYEE

Lưu ý rằng nếu chúng ta xóa từ khóa DISTINCT khỏi truy vấn SQL này, thì các bản sao sẽ không bị loại bỏ. Tùy chọn này không có sẵn trong đại số quan hệ chính thức, nhưng đại số có thể được mở rộng để bao gồm phép toán này và cho phép các mối quan hệ trở thành nhiều tập hợp; chúng tôi không thảo luận về các tiện ích mở rộng này ở đây.

1.3 Phép đổi tên (RENAME)

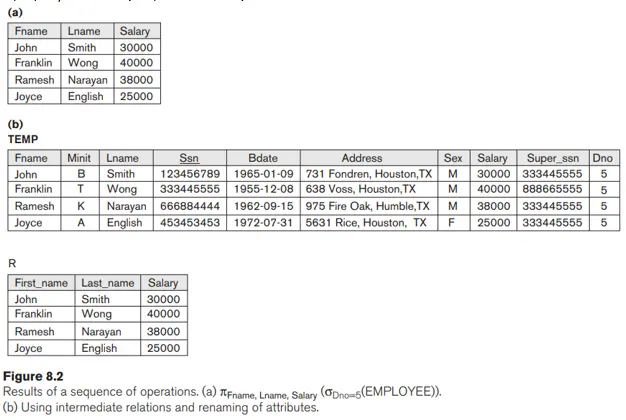
Các mối quan hệ được hiển thị trong Hình 8.1 mô tả kết quả hoạt động không có bất kỳ tên nào. Nói chung, đối với hầu hết các truy vấn, chúng ta cần lần lượt áp dụng một số phép toán đại số quan hệ. Hoặc chúng ta có thể viết các phép toán dưới dạng một biểu thức đại số quan hệ duy nhất bằng cách lồng các phép toán hoặc chúng ta có thể áp dụng từng phép toán một và tạo các quan hệ kết quả trung gian. Trong trường hợp sau, chúng ta phải đặt tên cho các quan hệ chứa các kết quả trung gian. Ví dụ, để lấy họ và tên, lương của tất cả các nhân viên làm việc trong bộ phận số 5, chúng ta phải áp dụng thao tác SELECT và PROJECT. Chúng ta có thể viết một biểu thức đại số quan hệ duy nhất, còn được gọi là biểu thức nội tuyến, như sau:

π_{Fname, Lname, Salary}(σDno=5(EMPLOYEE))

Hình 8.2(a) cho thấy kết quả của biểu thức đại số quan hệ nội tuyến này. Ngoài ra, chúng ta có thể hiển thị rõ ràng chuỗi các thao tác, đặt tên cho mỗi quan hệ trung gian và sử dụng thao tác gán, được biểu thị bằng ← (mũi tên trái), như sau:

DEP5_EMPS ← σ_Dno=5(EMPLOYEE)

RESULT ← π_{Fname, Lname, Salary}(DEP5_EMPS)

Đôi khi việc chia nhỏ một chuỗi các phép toán phức tạp bằng cách xác định các quan hệ kết quả trung gian sẽ đơn giản hơn là viết một biểu thức đại số quan hệ đơn lẻ. Chúng ta cũng có thể sử dụng kỹ thuật này để đổi tên các thuộc tính trong quan hệ trung gian và kết quả. Điều này có thể hữu ích liên quan đến các hoạt động phức tạp hơn như UNION và JOIN, như chúng ta sẽ thấy. Để đổi tên các thuộc tính trong một quan hệ, chúng ta chỉ cần liệt kê các tên thuộc tính mới trong ngoặc đơn, như trong ví dụ sau:

TEMP ← σ_Dno=5(EMPLOYEE)

R(First_name, Last_name, Salary) ← π_{Fname, Lname, Salary}(TEMP)

Hai thao tác này được minh họa trong Hình 8.2(b).

Nếu không áp dụng đổi tên, tên của các thuộc tính trong quan hệ kết quả của thao tác CHỌN sẽ giống với tên của các thuộc tính trong quan hệ ban đầu và theo cùng một thứ tự. Đối với thao tác PROJECT không đổi tên, quan hệ kết quả có tên thuộc tính giống như tên thuộc tính trong danh sách phép chiếu và theo cùng thứ tự xuất hiện trong danh sách

Chúng ta cũng có thể định nghĩa một phép toán RENAME chính thức—có thể đổi tên quan hệ hoặc tên thuộc tính hoặc cả hai—như một toán tử đơn hạng. Phép toán RENAME chung khi áp dụng cho quan hệ R bậc n được biểu thị bằng bất kỳ dạng nào trong ba dạng sau:

ρS(B1, B2, ... , Bn)(R) hoặc ρS(R) hoặc  ρ(B1, B2, ... , Bn)(R)

trong đó ký hiệu ρ (rho) được sử dụng để biểu thị toán tử RENAME, S là tên quan hệ mới và B1, B2, … , Bn là tên thuộc tính mới. Biểu thức đầu tiên đổi tên cả quan hệ và các thuộc tính của nó, biểu thức thứ hai chỉ đổi tên quan hệ và biểu thức thứ ba chỉ đổi tên các thuộc tính. Nếu các thuộc tính của R là (A1, A2, … , An) theo thứ tự đó, thì mỗi Ai được đổi tên thành Bi.

Trong SQL, một truy vấn duy nhất thường đại diện cho một biểu thức đại số quan hệ phức tạp. Đổi tên trong SQL được thực hiện bằng cách đặt bí danh bằng AS, như trong ví dụ sau:

SELECT 	E.Fname AS First_name, E.Lname AS Last_name, E.Salary AS Salary 
FROM 	EMPLOYEE AS E 
WHERE E.Dno=5,

2. Các phép toán quan hệ từ lý thuyết tập hợp

2.1 Phép toán UNION, INTERSECTION và MINUS

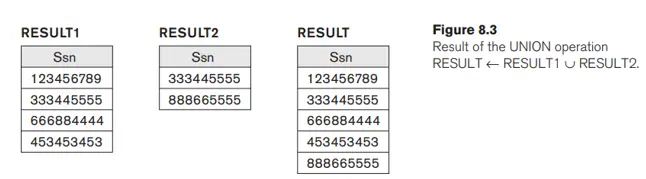
Nhóm các phép toán đại số quan hệ tiếp theo là các phép toán tiêu chuẩn trên các tập hợp. Ví dụ: để truy xuất số An sinh xã hội của tất cả nhân viên làm việc trong bộ phận 5 hoặc trực tiếp giám sát một nhân viên làm việc trong bộ phận 5, chúng ta có thể sử dụng thao tác UNION như sau:

DEP5_EMPS ← σ_Dno=5(EMPLOYEE)

RESULT1 ← π_Ssn(DEP5_EMPS)

RESULT2(Ssn) ← π_{Super_ssn}(DEP5_EMPS)

RESULT ← RESULT1 ∪ RESULT2

Mối quan hệ RESULT1 có Ssn của tất cả các nhân viên làm việc trong bộ phận 5, trong khi RESULT2 có Ssn của tất cả các nhân viên trực tiếp giám sát một nhân viên làm việc trong bộ phận 5. Phép toán UNION tạo ra các bộ nằm trong RESULT1 hoặc RESULT2 hoặc cả hai ( xem Hình 8.3) trong khi loại bỏ mọi trùng lặp. Do đó, giá trị Ssn '333445555' chỉ xuất hiện một lần trong kết quả.

Một số phép toán lý thuyết tập hợp được sử dụng để hợp nhất các phần tử của hai tập hợp theo nhiều cách khác nhau, bao gồm UNION, INTERSECTION và SET DIFFERENCE (còn gọi là MINUS hoặc EXCEPT). Đây là các thao tác nhị phân; nghĩa là, mỗi cái được áp dụng cho hai bộ (bộ). Khi các thao tác này được áp dụng cho cơ sở dữ liệu quan hệ, hai quan hệ mà bất kỳ thao tác nào trong số ba thao tác này được áp dụng phải có cùng loại bộ dữ liệu; điều kiện này đã được gọi là khả năng tương thích. Hai quan hệ R(A1, A2, … , An) và S(B1, B2, … , Bn) được gọi là tương thích hợp (hoặc tương thích kiểu) nếu chúng có cùng bậc n và nếu dom(Ai) = dom( bi) cho 1 ≤ i ≤ n. Điều này có nghĩa là hai quan hệ có cùng số thuộc tính và mỗi cặp thuộc tính tương ứng có cùng một miền.

Ta có thể định nghĩa ba phép toán UNION, INTERSECTION và SET DIFFERENCE trên hai quan hệ tương thích hợp R và S như sau:

• UNION: Kết quả của thao tác này, ký hiệu là R ∪ S, là một quan hệ bao gồm tất cả các bộ hoặc thuộc R hoặc thuộc S hoặc thuộc cả R và S. Các bộ trùng lặp bị loại bỏ
• INTERSECTION: Kết quả của phép toán này, ký hiệu là R ∩ S, là một quan hệ bao gồm tất cả các bộ thuộc cả R và S.
• SET DIFFERENCE (hoặc MINUS): Kết quả của thao tác này, ký hiệu là R – S, là một quan hệ bao gồm tất cả các bộ thuộc R nhưng không thuộc S.

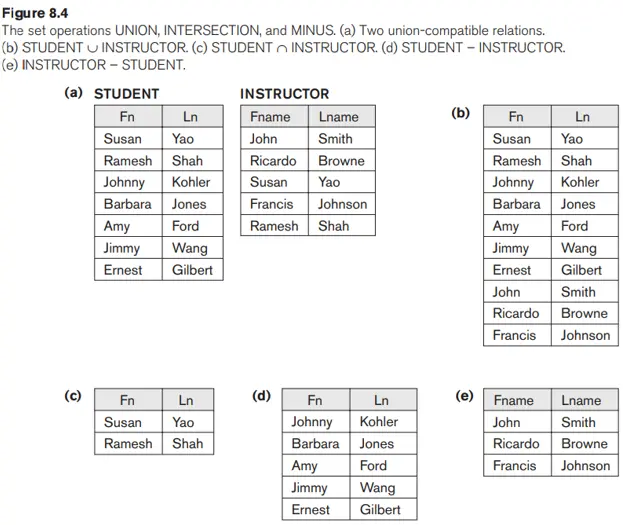
Chúng ta sẽ áp dụng quy ước rằng quan hệ kết quả có cùng tên thuộc tính với quan hệ đầu tiên R. Luôn có thể đổi tên các thuộc tính trong kết quả bằng cách sử dụng toán tử đổi tên.

Hình 8.4 minh họa ba hoạt động. Mối quan hệ STUDENT và INSTRUCTOR trong Hình 8.4(a) tương thích với phép hợp và các bộ của chúng lần lượt biểu thị tên của sinh viên và tên của người hướng dẫn. Kết quả của thao tác UNION trong Hình 8.4(b) hiển thị tên của tất cả học viên và giáo viên hướng dẫn. Lưu ý rằng các bộ dữ liệu trùng lặp chỉ xuất hiện một lần trong kết quả. Kết quả của phép toán INTERSECTION (Hình 8.4(c)) chỉ bao gồm những người vừa là sinh viên vừa là giáo viên hướng dẫn

Lưu ý rằng cả UNION và INTERSECTION đều là các phép toán giao hoán; đó là,

R ∪ S = S ∪ R và R ∩ S = S ∩ R

Cả UNION và INTERSECTION đều có thể được coi là phép toán n-ary áp dụng cho bất kỳ số lượng quan hệ nào bởi vì cả hai cũng là hoạt động kết hợp; đó là,

R ∪ (S ∪ T ) = (R ∪ S) ∪ T và (R ∩ S) ∩ T = R ∩ (S ∩ T)

Phép toán MINUS không có tính chất giao hoán

R − S ≠ S – R

Hình 8.4(d) hiển thị tên của sinh viên không phải là giảng viên và Hình 8.4(e) hiển thị tên của giảng viên không phải là sinh viên

Lưu ý rằng INTERSECTION có thể được biểu diễn dưới dạng hợp và hiệu như sau:

R ∩ S = ((R ∪ S) − (R − S)) − (S − R)

Trong SQL, có ba thao tác—UNION, INTERSECT và EXCEPT—tương ứng với các thao tác tập hợp được mô tả ở đây. Ngoài ra, có nhiều hoạt động (UNION ALL, INTERSECT ALL và EXCEPT ALL) không loại bỏ các bản sao

2.2 Caterian Product (Phép Kết)

Tiếp theo, chúng ta thảo luận về phép toán CARTESIAN PRODUCT— còn được gọi là CROSS JOIN được biểu thị bằng ×. Đây cũng là một phép toán tập hợp nhị phân, nhưng các quan hệ mà nó được áp dụng không nhất thiết phải tương thích với phép hợp. Ở dạng nhị phân, thao tác tập hợp này tạo ra một phần tử mới bằng cách kết hợp mọi phần tử (bộ) từ một quan hệ với mọi phần tử (bộ) từ quan hệ khác. Nói chung, kết quả của R(A1, A2, … , An) × S(B1, B2, … , Bm) là một quan hệ Q có bậc n + m thuộc tính Q(A1, A2, …, An, B1, B2 , … , Bm), theo thứ tự đó. Kết quả là quan hệ Q có một bộ cho mỗi tổ hợp các bộ—một từ R và một từ S. Do đó, nếu R có nR bộ (ký hiệu là |R| = nR), và S có nS bộ, thì R × S sẽ có bộ dữ liệu nR * nS.

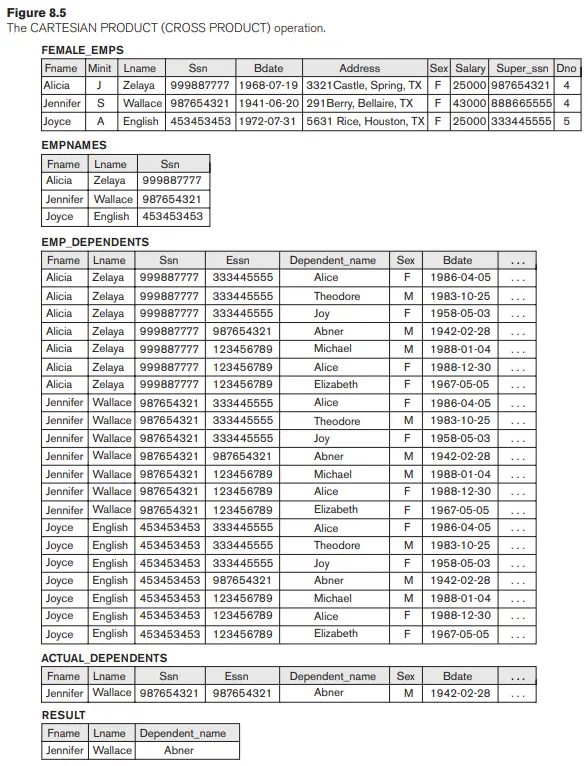
Thao tác CARTESIAN PRODUCT n-ary là một phần mở rộng của khái niệm trên, nó tạo ra các bộ mới bằng cách nối tất cả các kết hợp có thể có của các bộ từ n quan hệ cơ bản. Thao tác CARTESIAN PRODUCT được áp dụng bởi chính nó nói chung là vô nghĩa. Nó chủ yếu hữu ích khi được theo sau bởi một lựa chọn phù hợp với các giá trị của các thuộc tính đến từ các quan hệ thành phần. Ví dụ: giả sử rằng chúng tôi muốn truy xuất danh sách tên của từng người phụ thuộc của nhân viên nữ. Chúng ta có thể làm điều này như sau:

FEMALE_EMPS ← σ_Sex=‘F’(EMPLOYEE)

EMPNAMES ← π_{Fname, Lname, Ssn}(FEMALE_EMPS)

EMP_DEPENDENTS ← EMPNAMES × DEPENDENT

ACTUAL_DEPENDENTS ← σ_Ssn=Essn(EMP_DEPENDENTS)

RESULT ← π_{Fname, Lname, Dependent_name}(ACTUAL_DEPENDENTS)

Các quan hệ kết quả từ chuỗi hoạt động này được thể hiện trong Hình 8.5. Mối quan hệ EMP_DEPENDENTS là kết quả của việc áp dụng phép toán CARTESIAN PRODUCT cho EMPNAMES từ Hình 8.5 với DEPENDENT từ Hình 5.6. Trong EMP_DEPENDENTS, mọi bộ từ EMPNAMES được kết hợp với mọi bộ từ DEPENDENT, cho kết quả không có nhiều ý nghĩa (mọi người phụ thuộc được kết hợp với mọi nhân viên nữ). Chúng tôi chỉ muốn kết hợp một bộ dữ liệu nhân viên nữ với những người phụ thuộc cụ thể của cô ấy—cụ thể là các bộ dữ liệu DEPENDENT có giá trị Essn khớp với giá trị Ssn của bộ dữ liệu EMPLOYEE. Mối quan hệ ACTUAL_DEPENDENTS thực hiện điều này. Mối quan hệ EMP_DEPENDENTS là một ví dụ điển hình về trường hợp đại số quan hệ có thể được áp dụng chính xác để mang lại kết quả không có ý nghĩa gì cả. Người dùng có trách nhiệm đảm bảo chỉ áp dụng các phép toán có ý nghĩa cho các mối quan hệ.

CARTESIAN PRODUCT  tạo ra các bộ với các thuộc tính kết hợp của hai quan hệ. Chúng ta chỉ có thể SELECT các bộ liên quan từ hai quan hệ bằng cách chỉ định một điều kiện lựa chọn thích hợp sau tích Đề các, như chúng ta đã làm trong ví dụ trước. Vì trình tự CARTESIAN PRODUCT theo sau là SELECT này được sử dụng khá phổ biến để kết hợp các bộ dữ liệu có liên quan từ hai quan hệ, nên một phép toán đặc biệt, được gọi là JOIN, đã được tạo để chỉ định trình tự này là một phép toán đơn lẻ. Chúng tôi thảo luận về hoạt động JIN tiếp theo.

Trong SQL, CARTESIAN PRODUCT có thể được thực hiện bằng cách sử dụng tùy chọn CROSS PRODUCT trong các bảng đã tham gia. Ngoài ra, nếu có hai bảng trong mệnh đề FROM và không có điều kiện nối tương ứng trong mệnh đề WHERE của truy vấn SQL, thì kết quả cũng sẽ là CARTESIAN PRODUCT của hai bảng.

3. Các phép quan hệ nhị phân JOIN và DIVISION

3.1 Phép JOIN

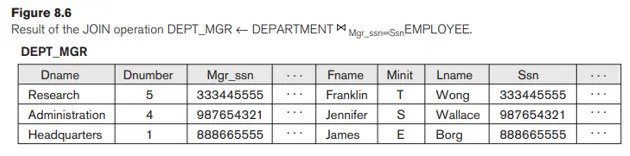
Thao tác JOIN, ký hiệu là ⋈, được sử dụng để kết hợp các bộ dữ liệu liên quan từ hai quan hệ thành các bộ dữ liệu "dài hơn" đơn lẻ. Thao tác này rất quan trọng đối với bất kỳ cơ sở dữ liệu quan hệ nào có nhiều hơn một quan hệ vì nó cho phép chúng ta xử lý các mối quan hệ giữa các quan hệ. Để minh họa JOIN, giả sử rằng chúng tôi muốn lấy tên của người quản lý của từng bộ phận. Để có được tên của người quản lý, chúng ta cần kết hợp từng bộ dữ liệu của bộ phận với bộ dữ liệu của nhân viên có giá trị Ssn khớp với giá trị Mgr_ssn trong bộ dữ liệu của bộ phận. Chúng tôi thực hiện điều này bằng cách sử dụng thao tác JOIN và sau đó chiếu kết quả lên các thuộc tính cần thiết, như sau:

DEPT_MGR ← DEPARTMENT Mgr_ssn=Ssn

EMPLOYEE RESULT ← πDname, Lname, Fname(DEPT_MGR)

Thao tác đầu tiên được minh họa trong Hình 8.6. Lưu ý rằng Mgr_ssn là khóa ngoại của quan hệ DEPARTMENT tham chiếu đến Ssn, khóa chính của quan hệ EMPLOYEE. Ràng buộc toàn vẹn tham chiếu này đóng vai trò trong việc có các bộ phù hợp trong quan hệ được tham chiếu EMPLOYEE.

Thao tác JOIN có thể được chỉ định dưới dạng thao tác CARTESIAN JOIN, sau đó là thao tác SELECT. Tuy nhiên, JOIN rất quan trọng vì nó được sử dụng thường xuyên khi chỉ định các truy vấn cơ sở dữ liệu. Xem xét ví dụ CARTESIAN JOIN trước đó, bao gồm các chuỗi hoạt động sau:

EMP_DEPENDENTS ← EMPNAMES × DEPENDENT

ACTUAL_DEPENDENTS ← σ_Ssn=Essn(EMP_DEPENDENTS)

Hai thao tác này có thể được thay thế bằng một thao tác JOIN như sau:

ACTUAL_DEPENDENTS ← EMPNAMES ⋈_Ssn=EssnDEPENDENT

Dạng tổng quát của phép THAM GIA trên hai quan hệ R(A1, A2, … , An) và S(B1, B2, …, Bm) là

R ⋈_{<join condition>} S

Kết quả của phép JOIN là một quan hệ Q với n + m thuộc tính Q(A1, A2, …, An, B1, B2, …, Bm) theo thứ tự đó; Q có một bộ cho mỗi tổ hợp các bộ—một từ R và một từ S—bất cứ khi nào tổ hợp thỏa mãn điều kiện nối. Đây là sự khác biệt chính giữa CARTESIAN JOIN và JOIN. Trong JOIN, chỉ các tổ hợp bộ dữ liệu thỏa mãn điều kiện nối mới xuất hiện trong kết quả, trong khi trong CARTESIAN JOIN, tất cả các tổ hợp bộ dữ liệu đều được đưa vào kết quả. Điều kiện kết nối được xác định trên các thuộc tính từ hai quan hệ R và S và được đánh giá cho mỗi tổ hợp các bộ. Mỗi tổ hợp bộ mà điều kiện nối đánh giá là TRUE được bao gồm trong quan hệ kết quả Q dưới dạng một bộ kết hợp duy nhất.

Một điều kiện tham gia chung có dạng

<condition> AND <condition>  AND … AND <condition>

trong đó mỗi <condition> cái có dạng Ai θ Bj, Ai là thuộc tính của R, Bj là thuộc tính của S, Ai và Bj có cùng một miền và θ (theta) là một trong các toán tử so sánh {=,≥, ≠ }. Phép JOIN với điều kiện tham gia chung như vậy được gọi là THETA JOIN. Các bộ có thuộc tính nối là NULL hoặc có điều kiện nối là FALSE không xuất hiện trong kết quả. Theo nghĩa đó, thao tác JOIN không nhất thiết bảo toàn tất cả thông tin trong các quan hệ tham gia, bởi vì các bộ không được kết hợp với các bộ phù hợp trong quan hệ khác sẽ không xuất hiện trong kết quả.

3.2 Các biến thể của phép JOIN: EQUI JOIN và NATURAL JOIN

Cách sử dụng phổ biến nhất của JOIN liên quan đến các điều kiện tham gia chỉ với các phép so sánh bình đẳng. JOIN như vậy, trong đó toán tử so sánh duy nhất được sử dụng là =, được gọi là EQUI JOIN. Cả hai ví dụ trước đều là EQUI JOIN. Lưu ý rằng trong kết quả của một EQUI JOIN, chúng ta luôn có một hoặc nhiều cặp thuộc tính có giá trị giống hệt nhau trong mỗi bộ. Ví dụ, trong Hình 8.6, các giá trị của các thuộc tính Mgr_ssn và Ssn giống hệt nhau trong mọi bộ của DEPT_MGR (kết quả EQUI JOIN Ị) vì điều kiện nối đẳng thức được chỉ định trên hai thuộc tính này yêu cầu các giá trị phải giống hệt nhau trong mọi bộ trong kết quả. Bởi vì một trong mỗi cặp thuộc tính có giá trị giống hệt nhau là không cần thiết, nên một thao tác mới có tên là NATURAL JOIN—ký hiệu là *—được tạo để loại bỏ thuộc tính (thừa) thứ hai trong một điều kiện EQUI JOIN. Định nghĩa tiêu chuẩn của NATURAL JOIN  yêu cầu rằng hai thuộc tính nối (hoặc từng cặp thuộc tính nối) có cùng tên trong cả hai quan hệ. Nếu đây không phải là trường hợp, thao tác đổi tên được áp dụng trước

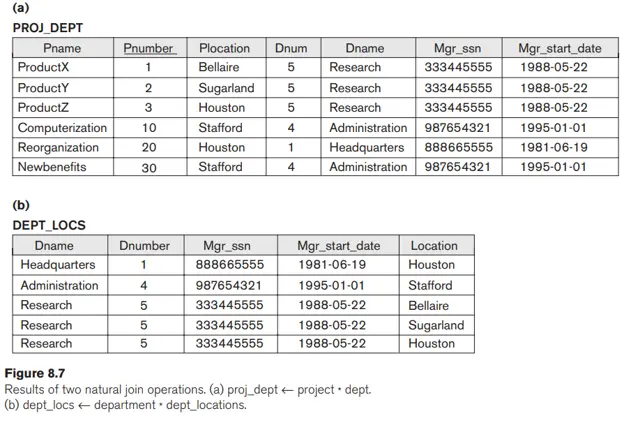
Giả sử chúng ta muốn kết hợp từng bộ PROJECT với bộ DEPARTMENT giám sát dự án. Trong ví dụ sau, trước tiên, chúng tôi đổi tên thuộc tính Dnumber của DEPARTMENT thành Dnum—để thuộc tính này có cùng tên với thuộc tính Dnum trong PROJECT—và sau đó chúng tôi áp dụng NATURAL JOIN:

PROJ_DEPT ← PROJECT * ρ_{(Dname, Dnum, Mgr_ssn, Mgr_start_date)}(DEPARTMENT)

Có thể thực hiện cùng một truy vấn theo hai bước bằng cách tạo một bảng trung gian DEPT như sau:

DEPT ← ρ_{(Dname, Dnum, Mgr_ssn, Mgr_start_date)}(DEPARTMENT) P

ROJ_DEPT ← PROJECT * DEPT

Thuộc tính Dnum được gọi là thuộc tính join cho thao tác NATURAL JOIN, bởi vì nó là thuộc tính duy nhất có cùng tên trong cả hai quan hệ. Mối quan hệ kết quả được minh họa trong Hình 8.7(a). Trong quan hệ PROJ_DEPT, mỗi bộ dữ liệu kết hợp bộ dữ liệu PROJECT với bộ dữ liệu DEPARTMENT cho bộ phận kiểm soát dự án, nhưng chỉ có một giá trị thuộc tính nối được giữ lại.

Nếu các thuộc tính mà natural join được chỉ định đã có cùng tên trong cả hai quan hệ, thì việc đổi tên là không cần thiết. Ví dụ: để áp dụng phép nối tự nhiên trên các thuộc tính Dnumber của DEPARTMENT và DEPT_LOCATIONS, chỉ cần viết

DEPT_LOCS ← DEPARTMENT * DEPT_LOCATIONS

Mối quan hệ kết quả được hiển thị trong Hình 8.7(b), kết hợp mỗi bộ phận với các vị trí của nó và có một bộ cho mỗi vị trí. Nói chung, điều kiện nối cho NATURAL JOIN được xây dựng bằng cách đánh đồng từng cặp thuộc tính nối có cùng tên trong hai quan hệ và kết hợp các điều kiện này với AND. Có thể có một danh sách các thuộc tính nối từ mỗi quan hệ và mỗi cặp tương ứng phải có cùng tên.

Lưu ý rằng nếu không có sự kết hợp nào của các bộ thỏa mãn điều kiện nối, thì kết quả của một phép JOIN là một quan hệ rỗng với các bộ bằng không. Nói chung, nếu R có nR bộ dữ liệu và S có nS bộ dữ liệu, kết quả của thao tác JOIN R S sẽ có từ 0 đến nR * nS bộ dữ liệu. Kích thước dự kiến của kết quả join chia cho kích thước tối đa nR * nS dẫn đến một tỷ lệ được gọi là độ chọn lọc join, đây là thuộc tính của từng điều kiện tham gia. Nếu không có điều kiện nối, tất cả các kết hợp của các bộ đủ điều kiện và JOIN hình thành CARTESIAN JION, còn được gọi là CROSS JOIN.

Như chúng ta có thể thấy, một thao tác JOIN đơn lẻ được sử dụng để kết hợp dữ liệu từ hai quan hệ sao cho thông tin liên quan có thể được trình bày trong một bảng. Các thao tác này còn được gọi là inner join, để phân biệt chúng với một biến thể phép nối khác được gọi là outer join. Một cách không chính thức, phép nối bên trong là một loại hoạt động so khớp và kết hợp được định nghĩa chính thức là sự kết hợp giữa CARTESIAN JOIN và SELECTION. Lưu ý rằng đôi khi một phép nối có thể được chỉ định giữa một quan hệ và chính nó, như chúng tôi sẽ minh họa trong phần sau. Thao tác NATURAL JOIN hoặc EQUIJOIN cũng có thể được chỉ định giữa nhiều bảng, dẫn đến phép nối n-way. Ví dụ, hãy xem xét phép nối ba chiều sau

((PROJECT ⋈ _Dnum=DnumberDEPARTMENT) ⋈_{Mgr_ssn=Ssn}EMPLOYEE)

Điều này kết hợp từng bộ dự án với bộ kiểm soát bộ phận của nó thành một bộ duy nhất và sau đó kết hợp bộ dữ liệu đó với bộ nhân viên là người quản lý bộ phận. Kết quả cuối cùng là một mối quan hệ hợp nhất trong đó mỗi bộ chứa thông tin kết hợp giữa bộ phận dự án-người quản lý dự án này.

Trong SQL, THAM GIA có thể được thực hiện theo nhiều cách khác nhau. Phương pháp đầu tiên là chỉ định trong mệnh đề WHERE, cùng với bất kỳ điều kiện lựa chọn nào khác. Điều này rất phổ biến và được minh họa bằng các truy vấn Q1, Q1A, Q1B, Q2 và Q8 trong các phần trước, cũng như bằng nhiều ví dụ truy vấn khác trong Chương 6 và 7. Cách thứ hai là sử dụng một quan hệ lồng nhau, như được minh họa bởi các truy vấn Q4A và Q16. Một cách khác là sử dụng khái niệm về các bảng đã nối, như được minh họa bởi các truy vấn Q1A, Q1B, Q8B và Q2A. Cấu trúc của các bảng đã nối đã được thêm vào SQL2 để cho phép người dùng chỉ định rõ ràng tất cả các kiểu nối khác nhau, vì các phương pháp khác bị hạn chế hơn. Nó cũng cho phép người dùng phân biệt rõ ràng điều kiện tham gia với điều kiện lựa chọn trong mệnh đề WHERE.

3.3 Tập hợp đầy đủ các phép toán đại số quan hệ

Người ta đã chỉ ra rằng tập hợp các phép toán đại số quan hệ {σ, π, ∪, ρ, –, ×} là một tập hợp đầy đủ; nghĩa là, bất kỳ phép toán đại số quan hệ gốc nào khác đều có thể được biểu diễn dưới dạng một chuỗi các phép toán từ tập hợp này. Ví dụ, phép toán INTERSECTION có thể được thể hiện bằng cách sử dụng UNION và MINUS như sau:

R ∩ S ≡ (R ∪ S) – ((R – S) ∪ (S – R))

Mặc dù, nói đúng ra, INTERSECTION là không bắt buộc, nhưng thật bất tiện khi chỉ định biểu thức phức tạp này mỗi khi chúng ta muốn chỉ định một phép giao. Một ví dụ khác, thao tác JOIN có thể được chỉ định là CARTESIAN JOIN theo sau là thao tác SELECT, như chúng ta đã thảo luận

R ⋈_<condition>S ≡ σ_<condition>(R × S)

Tương tự, một NATURAL JOIN có thể được chỉ định là một CARTESIAN JOIN được xử lý  RENAME và theo sau là các thao tác SELECT và PROJECT. Do đó, các thao tác JOIN khác nhau cũng không thực sự cần thiết đối với sức mạnh biểu đạt của đại số quan hệ. Tuy nhiên, chúng rất quan trọng để bao gồm các hoạt động riêng biệt vì chúng thuận tiện để sử dụng và thường được áp dụng trong các ứng dụng cơ sở dữ liệu. Các hoạt động khác đã được đưa vào đại số quan hệ cơ bản để thuận tiện hơn là cần thiết. Chúng ta thảo luận về một trong số này—phép DIVISION—trong phần tiếp theo

3.4 Phép chia quan hệ (DIVISION)

Phép toán DIVISION, ký hiệu là ÷, rất hữu ích cho một loại truy vấn đặc biệt đôi khi xảy ra trong các ứng dụng cơ sở dữ liệu. Một ví dụ là Truy xuất tên của các nhân viên làm việc trong tất cả các dự án mà ‘John Smith’ thực hiện. Để thể hiện truy vấn này bằng thao tác DIVISION, hãy tiến hành như sau. Đầu tiên, truy xuất danh sách các số dự án mà 'John Smith' làm việc trong quan hệ trung gian SMITH_PNOS:

SMITH ← σ_{Fname=‘John’ AND Lname=‘Smith’}(EMPLOYEE)

SMITH_PNOS ← π_Pno(WORKS_ON ⋈_Essn=SsnSMITH)

Tiếp theo, tạo một mối quan hệ bao gồm một bộ bất cứ khi nào nhân viên có Ssn là Essn làm việc trong dự án có mã số là Pno trong mối quan hệ trung gian SSN_PNOS:

SSN_PNOS ← π_{Essn, Pno}(WORKS_ON)

Cuối cùng, áp dụng phép toán DIVISION cho hai quan hệ, phép toán này cho số An sinh xã hội của nhân viên mong muốn:

SSNS(Ssn) ← SSN_PNOS ÷ SMITH_PNOS

RESULT ← π_{Fname, Lname}(SSNS * EMPLOYEE)

Các hoạt động trước đó được thể hiện trong Hình 8.8(a)

Nói chung, phép toán DIVISION được áp dụng cho hai quan hệ R(Z) ÷ S(X), trong đó các thuộc tính của S là tập con của các thuộc tính của R; nghĩa là X ⊆ Z. Gọi Y là tập các thuộc tính của R mà không phải là thuộc tính của S; nghĩa là, Y = Z – X (và do đó Z = X ∪ Y).

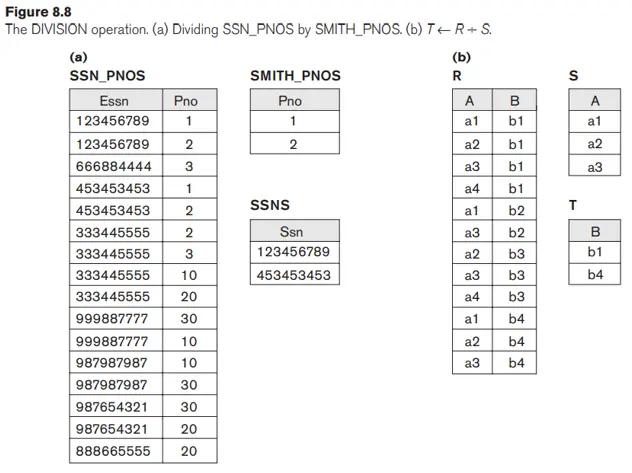
Kết quả của DIVISION là một quan hệ T(Y) bao gồm một bộ t nếu các bộ tR xuất hiện trong R với tR [Y] = t và với tR [X] = tS với mọi bộ tS trong S. Điều này có nghĩa là, đối với một bộ t xuất hiện trong kết quả T của DIVISION, các giá trị trong t phải xuất hiện trong R kết hợp với mọi bộ trong S. Lưu ý rằng trong công thức của phép toán DIVISION, các bộ trong quan hệ mẫu số S hạn chế quan hệ tử số R bằng cách chọn các bộ trong kết quả khớp với tất cả các giá trị có trong mẫu số. Không cần thiết phải biết những giá trị đó là gì vì chúng có thể được tính toán bằng một thao tác khác, như được minh họa trong quan hệ SMITH_PNOS trong ví dụ trước.

Hình 8.8(b) minh họa phép toán DIVISION trong đó X = {A}, Y = {B} và Z = {A, B}. Lưu ý rằng các bộ (giá trị) b1 và b4 xuất hiện trong R kết hợp với cả ba bộ trong S; đó là lý do tại sao chúng xuất hiện trong quan hệ kết quả T. Tất cả các giá trị khác của B trong R không xuất hiện với tất cả các bộ trong S và không được chọn: b2 không xuất hiện với a2 và b3 không xuất hiện với a1.

T1 ← πY(R)

T2 ← πY((S × T1) – R)

T ← T1 – T2

Hoạt động DIVISION được xác định để thuận tiện cho việc xử lý các truy vấn liên quan đến lượng hóa phổ quát, hoặc tất cả các điều kiện. Hầu hết các triển khai RDBMS với SQL là ngôn ngữ truy vấn chính không trực tiếp triển khai phép chia. SQL có cách xử lý đường vòng với loại truy vấn vừa được minh họa Bảng 8.1 liệt kê các phép toán đại số quan hệ cơ bản mà chúng ta đã thảo luận.

3.5 Cây truy vấn

Trong phần này, chúng tôi mô tả một ký hiệu thường được sử dụng trong các DBMS quan hệ (RDBMS) để biểu diễn các truy vấn bên trong. Ký hiệu được gọi là cây truy vấn hoặc đôi khi nó được gọi là cây đánh giá truy vấn hoặc cây thực hiện truy vấn. Nó bao gồm các phép toán đại số quan hệ đang được thực thi và được sử dụng như một cấu trúc dữ liệu khả thi cho biểu diễn bên trong của truy vấn trong RDBMS.

Cây truy vấn là một cấu trúc dữ liệu dạng cây tương ứng với một biểu thức đại số quan hệ. Nó biểu diễn các quan hệ đầu vào của truy vấn dưới dạng các nút lá của cây và biểu diễn các phép toán đại số quan hệ dưới dạng các nút bên trong. Việc thực thi cây truy vấn bao gồm thực hiện thao tác nút bên trong bất cứ khi nào các toán hạng của nó (được biểu thị bởi các nút con của nó) khả dụng và sau đó thay thế nút bên trong đó bằng mối quan hệ có được từ việc thực hiện thao tác. Việc thực thi kết thúc khi nút gốc được thực thi và tạo ra quan hệ kết quả cho truy vấn.

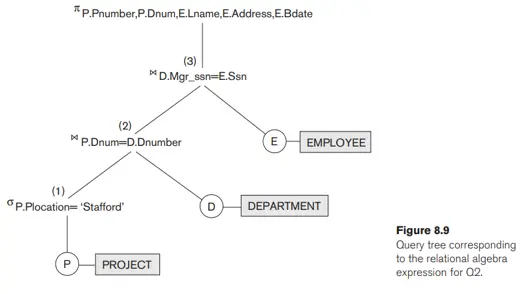
Hình 8.9 hiển thị một cây truy vấn cho Truy vấn 2: Đối với mọi dự án đặt tại 'Stafford', hãy liệt kê số dự án, số bộ phận kiểm soát và họ, địa chỉ và ngày sinh của người quản lý bộ phận. Truy vấn này được xác định trên lược đồ quan hệ của Hình 5.5 và tương ứng với biểu thức đại số quan hệ sau:

π_{Pnumber, Dnum, Lname, Address, Bdate}(((σ_{Plocation=‘Stafford’}(PROJECT)) ⋈_Dnum=Dnumber(DEPARTMENT)) Mgr_ssn=Ssn(EMPLOYEE))

Trong hình 8.9, ba nút lá P, D và E đại diện cho ba quan hệ PROJECT, DEPARTMENTvàEMPLOYEE. Các phép toán đại số quan hệ trong biểu thức được biểu diễn bằng các nút cây bên trong. Cây truy vấn biểu thị một thứ tự thực hiện rõ ràng theo nghĩa sau. Để thực hiện Q2, nút được đánh dấu (1) trong Hình 8.9 phải bắt đầu thực hiện trước nút (2) vì một số bộ kết quả của thao tác (1) phải có sẵn trước khi chúng ta có thể bắt đầu thực hiện thao tác (2). Tương tự, nút (2) phải bắt đầu thực hiện và tạo ra kết quả trước khi nút (3) có thể bắt đầu thực hiện, v.v. Nói chung, một cây truy vấn cung cấp một biểu diễn trực quan tốt và sự hiểu biết về truy vấn theo các phép toán quan hệ mà nó sử dụng và được khuyến nghị như một phương tiện bổ sung để biểu diễn các truy vấn trong đại số quan hệ. Chúng ta sẽ xem xét lại cây truy vấn khi thảo luận về quá trình xử lý và tối ưu hóa truy vấn trong Chương 18 và 19

4. Các phép quan hệ bổ sung

Một số yêu cầu cơ sở dữ liệu chung—cần thiết trong các ứng dụng thương mại cho RDBMS—không thể thực hiện được với các phép toán đại số quan hệ ban đầu được mô tả trong Phần 1 đến 3. Trong phần này, chúng tôi xác định các hoạt động bổ sung để thể hiện các yêu cầu này. Các phép toán này nâng cao sức mạnh biểu đạt của đại số quan hệ ban đầu

4.1 Phép chiếu tổng quát

Phép chiếu tổng quát mở rộng phép chiếu bằng cách cho phép đưa chức năng của các thuộc tính vào danh sách phép chiếu. Hình thức tổng quát có thể được thể hiện như sau:

π_{F1, F2, ..., Fn} (R)

trong đó F1, F2, …, Fn được thực hiện trên các thuộc tính liên quan đến R và có thể liên quan đến các phép toán số học và các giá trị không đổi. Thao tác này hữu ích khi phát triển các báo cáo trong đó các giá trị được tính phải được tạo trong các cột của kết quả truy vấn

Ví dụ, xem xét mối quan hệ

EMPLOYEE (Ssn, Salary, Deduction, Years_service)

Một báo cáo có thể được yêu cầu để hiển thị

Net Salary = Salary – Deduction,

Bonus = 2000 * Years_service, and

Tax = 0.25 * Salary

Sau đó, một phép chiếu tổng quát kết hợp với đổi tên có thể được sử dụng như sau:

REPORT ← ρ_{(Ssn, Net_salary, Bonus, Tax)(πSsn, Salary – Deduction, 2000 * Years_service, 0.25 * Salary}(EMPLOYEE))

4.2 Hàm tổng hợp và thao tác gôm nhóm

Một loại yêu cầu khác không thể biểu thị được trong đại số quan hệ cơ bản là chỉ định các hàm tổng hợp toán học trên các tập giá trị từ cơ sở dữ liệu. Ví dụ về các hàm như vậy bao gồm truy xuất mức lương trung bình hoặc tổng của tất cả nhân viên hoặc tổng số bộ dữ liệu nhân viên. Các hàm này được sử dụng trong các truy vấn thống kê đơn giản tóm tắt thông tin từ các bộ cơ sở dữ liệu. Các hàm phổ biến được áp dụng cho tập hợp các giá trị số bao gồm SUM, AVERAGE, MAXIMUM, và MINIMUM. Hàm COUNT được sử dụng để đếm các bộ dữ liệu hoặc giá trị

Một loại yêu cầu phổ biến khác liên quan đến việc nhóm các bộ trong một quan hệ theo giá trị của một số thuộc tính của chúng và sau đó áp dụng một hàm tổng hợp độc lập cho từng nhóm. Một ví dụ sẽ là nhóm các bộ dữ liệu EMPLOYEE theo Dno để mỗi nhóm bao gồm các bộ dữ liệu dành cho nhân viên làm việc trong cùng một bộ phận. Sau đó, chúng tôi có thể liệt kê từng giá trị Dno cùng với mức lương trung bình của nhân viên trong bộ phận hoặc số lượng nhân viên làm việc trong bộ phận.

Chúng ta có thể định nghĩa một thao tác AGGREGATE FUNCTION, sử dụng ký hiệu I (phát âm là chữ F), để chỉ định các loại yêu cầu này như sau

_{<grouping attributes>}ℑ_{<function list>} (R)

trong đó <grouping attributes> là danh sách các thuộc tính của quan hệ được chỉ định trong R <function list> là danh sách các cặp (<function> <attribute>) Trong mỗi cặp như vậy, <function> là một trong các hàm được phép—chẳng hạn như SUM, AVERAGE, MAXIMUM, MINIMUM, COUNT—và <attribute> là một thuộc tính của quan hệ được chỉ định bởi R. Quan hệ kết quả có các thuộc tính nhóm cộng với một thuộc tính cho mỗi phần tử trong danh sách chức năng. Ví dụ: để truy xuất từng mã số phòng ban, số lượng nhân viên trong phòng ban và mức lương trung bình của họ, đồng thời đổi tên các thuộc tính kết quả như được chỉ ra bên dưới, chúng tôi viết:

ρ_{R(Dno, No_of_employees, Average_sal)} (_Dno ℑ _{COUNT Ssn, AVERAGE Salary} (EMPLOYEE))

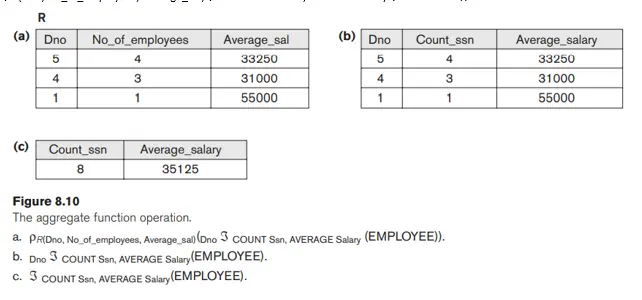
Kết quả của thao tác này trên quan hệ EMPLOYEE của Hình 5.6 được thể hiện trong Hình 8.10(a).

Trong ví dụ trước, chúng ta đã chỉ định một danh sách các tên thuộc tính—nằm giữa các dấu ngoặc đơn trong thao tác RENAME—cho quan hệ kết quả R. Nếu không áp dụng đổi tên, thì mỗi thuộc tính của các mối quan hệ kết quả tương ứng với danh sách hàm sẽ là phép nối của tên hàm với tên thuộc tính ở dạng <function>_<attribute>. Ví dụ, Hình 8.10(b) hiển thị kết quả của thao tác sau

_Dno ℑ _{COUNT Ssn, AVERAGE Salary}(EMPLOYEE)

Nếu không có thuộc tính nhóm nào được chỉ định, thì các hàm được áp dụng cho tất cả các bộ trong quan hệ, do đó, quan hệ kết quả chỉ có một bộ duy nhất. Ví dụ, Hình 8.10(c) thể hiện kết quả của thao tác sau:

ℑ _{COUNT Ssn, AVERAGE Salary}(EMPLOYEE)

Điều quan trọng cần lưu ý là nhìn chung, các bản sao không bị loại bỏ khi áp dụng hàm tổng hợp như SUM và AVERAGE. Tuy nhiên, các giá trị NULL không được xem xét trong tập hợp, như chúng ta đã thảo luận. Điều đáng nhấn mạnh là kết quả của việc áp dụng một hàm tổng hợp là một quan hệ, không phải là một số vô hướng—ngay cả khi nó có một giá trị duy nhất. Điều này làm cho đại số quan hệ trở thành một hệ thống toán học khép kín.

4.3 Đệ quy

Một kiểu phép toán khác, nói chung, không thể xác định được trong đại số quan hệ gốc cơ bản là phép đóng đệ quy. Thao tác này được áp dụng cho mối quan hệ đệ quy giữa các bộ cùng loại, chẳng hạn như mối quan hệ giữa nhân viên và người giám sát. Mối quan hệ này được mô tả bởi khóa ngoại Super_ssn của quan hệ EMPLOYEE trong Hình 5.5 và 5.6, và nó liên kết mỗi bộ nhân viên (trong vai trò người giám sát) với bộ nhân viên khác (trong vai trò người giám sát). Một ví dụ về thao tác đệ quy là truy xuất tất cả những người được giám sát của một nhân viên e ở tất cả các cấp—nghĩa là tất cả nhân viên e′ được giám sát trực tiếp bởi e, tất cả nhân viên e′ℑ được giám sát trực tiếp bởi từng nhân viên e′, tất cả nhân viên e″′ trực tiếp được giám sát bởi từng nhân viên e″, v.v.

Tương đối đơn giản trong đại số quan hệ để xác định tất cả các nhân viên được giám sát bởi e ở một cấp độ cụ thể bằng cách tham gia bảng với chính nó một hoặc nhiều lần. Tuy nhiên, rất khó để xác định cụ thể tất cả những người được giám sát ở tất cả các cấp. Ví dụ: để chỉ định Ssns của tất cả nhân viên e′ được giám sát trực tiếp—ở cấp một—bởi nhân viên e có tên là 'James Borg' (xem Hình 5.6), chúng ta có thể áp dụng thao tác sau:

BORG_SSN ← π_Ssn(σ_{Fname=‘James’ AND Lname=‘Borg’}(EMPLOYEE))

SUPERVISION(Ssn1, Ssn2) ← π_{Ssn,Super_ssn}(EMPLOYEE)

RESULT1(Ssn) ← π_Ssn1(SUPERVISION ⋈_Ssn2=SsnBORG_SSN)

Để truy xuất tất cả nhân viên được giám sát bởi Borg ở cấp 2—nghĩa là tất cả nhân viên e″ được giám sát bởi một số nhân viên e′ được Borg trực tiếp giám sát—chúng ta có thể áp dụng một JOIN khác cho kết quả của truy vấn đầu tiên, như sau:

RESULT2(Ssn) ← π_Ssn1(SUPERVISION ⋈_Ssn2=SsnRESULT1)

Để cả hai nhóm nhân viên được giám sát ở cấp độ 1 và 2 bởi 'James Borg', chúng ta có thể áp dụng thao tác UNION cho hai kết quả, như sau:

RESULT ← RESULT2 ∪ RESULT1

Kết quả của các truy vấn này được minh họa trong Hình 8.11. Mặc dù có thể truy xuất nhân viên ở mỗi cấp và sau đó lấy UNION của họ, nhưng nói chung, chúng tôi không thể chỉ định một truy vấn chẳng hạn như “truy xuất những người được giám sát của 'James Borg' ở tất cả các cấp” mà không sử dụng cơ chế lặp trừ khi chúng tôi biết tối đa số lượng cấp độ. Một hoạt động được gọi là sự đóng cửa chuyển tiếp của các mối quan hệ đã được đề xuất để tính toán mối quan hệ đệ quy cho đến khi đệ quy ra đời

4.4 OUTER JOIN

Tiếp theo, chúng tôi thảo luận về một số phần mở rộng bổ sung cho thao tác THAM GIA cần thiết để chỉ định một số loại truy vấn nhất định. Các thao tác JOIN đã mô tả các bộ so khớp trước đó thỏa mãn điều kiện nối. Ví dụ: đối với thao tác NATURAL JOIN R * S, chỉ các bộ từ R có các bộ phù hợp trong S—và ngược lại—xuất hiện trong kết quả. Do đó, các bộ không có bộ phù hợp (hoặc có liên quan) sẽ bị loại khỏi kết quả JOIN. Các bộ có giá trị NULL trong thuộc tính nối cũng bị loại bỏ. Kiểu nối này, trong đó các bộ không khớp bị loại bỏ, được gọi là INNER JOIN. Các thao tác nối mà chúng ta đã mô tả trước đó trong Phần 8.3 đều là INNER JOIN. Điều này dẫn đến việc mất thông tin nếu người dùng muốn kết quả của JOIN bao gồm tất cả các bộ trong một hoặc nhiều quan hệ thành phần

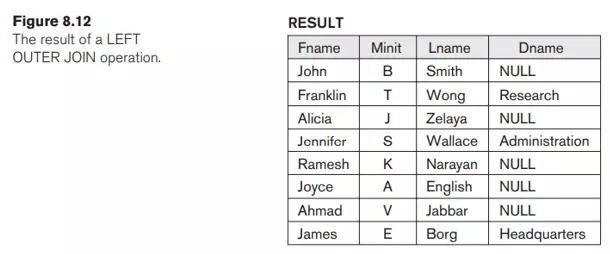
Một tập hợp các thao tác, được gọi là phép nối ngoài, được phát triển cho trường hợp người dùng muốn giữ tất cả các bộ trong R, hoặc tất cả các bộ trong S, hoặc tất cả các bộ trong cả hai quan hệ trong kết quả của phép JOIN, bất kể có hay không. chúng có các bộ phù hợp trong quan hệ khác. Điều này đáp ứng nhu cầu của các truy vấn trong đó các bộ dữ liệu từ hai bảng sẽ được kết hợp bằng cách khớp các hàng tương ứng, nhưng không làm mất bất kỳ bộ dữ liệu nào do thiếu các giá trị khớp. Ví dụ: giả sử rằng chúng tôi muốn có một danh sách tất cả tên nhân viên cũng như tên của các bộ phận mà họ quản lý nếu họ tình cờ quản lý một bộ phận; nếu họ không quản lý một cái, chúng ta có thể chỉ ra nó bằng giá trị NULL. Ta có thể áp dụng một phép toán LEFT OUTER JOIN, ký hiệu là ⋊, để lấy kết quả như sau:

TEMP ← (EMPLOYEE ⋊_{Ssn=Mgr_ssn}DEPARTMENT)

RESULT ← π_{Fname, Minit, Lname, Dname}(TEMP)

Phép toán LEFT OUTER JOIN giữ mọi bộ trong quan hệ đầu tiên hoặc bên trái R trong R S; nếu không tìm thấy bộ phù hợp nào trong S, thì các thuộc tính của S trong kết quả nối được điền hoặc đệm bằng các giá trị NULL. Kết quả của các thao tác này được thể hiện trong Hình 8.12.

Một thao tác tương tự, RIGHT OUTER JOIN, ký hiệu là ⋉, giữ mọi bộ trong quan hệ thứ hai hoặc bên phải S trong kết quả của R ⋉ S. Thao tác thứ ba, FULL OUTER JOIN, giữ tất cả các bộ ở cả bên trái và bên phải. quan hệ bên phải khi không tìm thấy bộ dữ liệu phù hợp nào, đệm chúng bằng giá trị NULL nếu cần. Ba phép nối outer join này là một phần của tiêu chuẩn SQL2. Các phép toán này được cung cấp sau đó như một phần mở rộng của đại số quan hệ để đáp ứng nhu cầu điển hình trong các ứng dụng kinh doanh để hiển thị thông tin liên quan từ nhiều bảng một cách thấu đáo. Đôi khi cần có báo cáo đầy đủ về dữ liệu từ nhiều bảng cho dù có giá trị khớp hay không

4.5 Outer UNION

Phép toán OUTER UNION được phát triển để lấy phép hợp của các bộ từ hai quan hệ có một số thuộc tính chung nhưng không tương thích với phép hợp (kiểu). Thao tác này sẽ lấy UNION của các bộ trong hai quan hệ R(X, Y) và S(X, Z) tương thích một phần, nghĩa là chỉ một số thuộc tính của chúng, giả sử X, là tương thích với phép hợp. Các thuộc tính tương thích với phép hợp chỉ được biểu diễn một lần trong kết quả và những thuộc tính không tương thích với phép hợp từ một trong hai quan hệ cũng được giữ trong quan hệ kết quả T(X, Y, Z). Do đó, nó giống như một FULL OUTER JOIN trên các thuộc tính chung

Hai bộ t1 trong R và t2 trong S được gọi là khớp nếu t1[X] = t2[X]. Chúng sẽ được kết hợp (liên kết) thành một bộ duy nhất trong t. Các bộ trong một trong hai quan hệ không có bộ phù hợp trong quan hệ kia được đệm bằng các giá trị NULL. Ví dụ, một OUTER UNION có thể được áp dụng cho hai quan hệ có lược đồ là STUDENT (Name, Ssn, Department, Advisor) và INSTRUCTOR(Name, Ssn, Department, Rank). Các bộ từ hai quan hệ được so khớp dựa trên việc có cùng một tổ hợp giá trị của các thuộc tính được chia sẻ— Name, Ssn, Department. Mối quan hệ kết quả, STUDENT_OR_INSTRUCTOR, sẽ có các thuộc tính sau:

STUDENT_OR_INSTRUCTOR(Name, Ssn, Department, Advisor, Rank)

Tất cả các bộ dữ liệu từ cả hai quan hệ đều được bao gồm trong kết quả, nhưng các bộ dữ liệu có cùng tổ hợp (Tên, Ssn, Bộ phận) sẽ chỉ xuất hiện một lần trong kết quả. Các bộ chỉ xuất hiện trong STUDENT sẽ có NULL cho thuộc tính Xếp hạng, trong khi các bộ chỉ xuất hiện trong INSTRUCTOR sẽ có NULL cho thuộc tính Advisor. Một bộ tồn tại trong cả hai quan hệ, đại diện cho một sinh viên đồng thời là một giảng viên, sẽ có các giá trị cho tất cả các thuộc tính của nó.

Lưu ý rằng cùng một người vẫn có thể xuất hiện hai lần trong kết quả. Ví dụ: chúng ta có thể có một sinh viên tốt nghiệp khoa Toán là giảng viên khoa Khoa học Máy tính. Mặc dù hai bộ đại diện cho người đó trong STUDENT và INSTRUCTOR sẽ có cùng giá trị (Name, Ssn), nhưng chúng sẽ không thống nhất về giá trị Department, và do đó sẽ không khớp. Điều này là do Department có hai ý nghĩa khác nhau trong STUDENT (bộ phận nơi người đó học) và INSTRUCTOR (bộ phận nơi người đó được thuê làm người hướng dẫn). Nếu chúng ta chỉ muốn áp dụng OUTER UNION dựa trên cùng một kết hợp (Name, Ssn), chúng ta nên đổi tên thuộc tính Department trong mỗi bảng để phản ánh rằng chúng có ý nghĩa khác nhau và chỉ định chúng không phải là một phần của các thuộc tính tương thích với union. Ví dụ: chúng ta có thể đổi tên các thuộc tính thành MajorDept trong STUDENT và WorkDept trong INSTRUCTOR

5. Ví dụ về truy vấn trong đại số quan hệ

Sau đây là các ví dụ bổ sung để minh họa việc sử dụng các phép toán đại số quan hệ. Tất cả các ví dụ tham khảo cơ sở dữ liệu trong Hình 5.6. Nói chung, cùng một truy vấn có thể được phát biểu theo nhiều cách bằng nhiều thao tác khác nhau. Chúng tôi sẽ nêu từng truy vấn theo một cách và để người đọc tự đưa ra các công thức tương đương

Truy vấn 1. Truy xuất tên và địa chỉ của tất cả nhân viên làm việc cho bộ phận 'Research’

RESEARCH_DEPT ← σ_{Dname=‘Research’}(DEPARTMENT)

RESEARCH_EMPS ← (RESEARCH_DEPT ⋈_Dnumber=DnoEMPLOYEE)

RESULT ← π_{Fname, Lname, Address}(RESEARCH_EMPS)

Khi được viết thành 1 hàng, truy vấn này trở thành:

π_{Fname, Lname, Address} (σ_{Dname=‘Research’}(DEPARTMENT ⋈_Dnumber=Dno(EMPLOYEE))

Truy vấn này có thể được chỉ định theo những cách khác; ví dụ: thứ tự của các thao tác JOIN và SELECT có thể bị đảo ngược hoặc JOIN có thể được thay thế bằng NATURAL JOIN sau khi đổi tên một trong các thuộc tính nối để khớp với tên thuộc tính nối khác.

Truy vấn 2. Đối với mọi dự án đặt tại ‘Stafford’, hãy liệt kê số dự án, số bộ phận kiểm soát và họ, địa chỉ và ngày sinh của người quản lý bộ phận.

STAFFORD_PROJS ← σ_{Plocation=‘Stafford’}(PROJECT)

CONTR_DEPTS ← (STAFFORD_PROJS ⋈_Dnum=DnumberDEPARTMENT)

PROJ_DEPT_MGRS ← (CONTR_DEPTS ⋈_{Mgr_ssn=Ssn}EMPLOYEE)

RESULT ← π_{Pnumber, Dnum, Lname, Address, Bdate}(PROJ_DEPT_MGRS)

Trong ví dụ này, trước tiên chúng tôi chọn các dự án ở Stafford, sau đó kết hợp chúng với các bộ phận kiểm soát của chúng, sau đó kết hợp kết quả với các nhà quản lý bộ phận. Cuối cùng, chúng tôi áp dụng một phép chiếu cho các thuộc tính mong muốn

Truy vấn 3. Tìm tên của các nhân viên làm việc trong tất cả các dự án do bộ phận số 5 kiểm soát.

DEPT5_PROJS ← ρ_(Pno)(π_Pnumber(σ_Dnum=5(PROJECT)))

EMP_PROJ ← ρ_{(Ssn, Pno)}(π_{Essn, Pno}(WORKS_ON))

RESULT_EMP_SSNS ← EMP_PROJ ÷ DEPT5_PROJS

RESULT ← π_{Lname, Fname}(RESULT_EMP_SSNS * EMPLOYEE)

Trong truy vấn này, trước tiên chúng ta tạo một bảng DEPT5_PROJS chứa số dự án của tất cả các dự án do bộ phận 5 kiểm soát. Sau đó, chúng ta tạo một bảng EMP_PROJ chứa các bộ dữ liệu (Ssn, Pno) và áp dụng thao tác chia. Lưu ý rằng chúng tôi đã đổi tên các thuộc tính để chúng sẽ được sử dụng chính xác trong phép chia. Cuối cùng, chúng ta nối kết quả của phép chia, chỉ chứa các giá trị Ssn, với bảng EMPLOYEE để lấy các thuộc tính Fname, Lname từ EMPLOYEE.

Truy vấn 4. Lập danh sách số dự án cho các dự án liên quan đến một nhân viên có họ là 'Smith', với tư cách là công nhân hoặc quản lý của bộ phận kiểm soát dự án.

SMITHS(Essn) ← π_Ssn (σ_{Lname=‘Smith’}(EMPLOYEE))

SMITH_WORKER_PROJS ← π_Pno(WORKS_ON * SMITHS)

MGRS ← π_{Lname, Dnumber}(EMPLOYEE ⋈_{Ssn=Mgr_ssn}DEPARTMENT)

SMITH_MANAGED_DEPTS(Dnum) ← π_Dnumber (σ_{Lname=‘Smith’}(MGRS))

SMITH_MGR_PROJS(Pno) ← π_Pnumber(SMITH_MANAGED_DEPTS * PROJECT)

RESULT ← (SMITH_WORKER_PROJS ∪ SMITH_MGR_PROJS)

Trong truy vấn này, chúng tôi đã truy xuất số dự án cho các dự án có sự tham gia của một nhân viên tên Smith với tư cách là công nhân trong SMITH_WORKER_PROJS. Sau đó, chúng tôi đã truy xuất số dự án cho các dự án có sự tham gia của một nhân viên tên Smith với tư cách là người quản lý bộ phận kiểm soát dự án trong SMITH_MGR_PROJS. Cuối cùng, chúng tôi đã áp dụng thao tác UNION trên SMITH_WORKER_PROJS và SMITH_MGR_PROJS. Nếu viết trong một dòng, truy vấn này trở thành:

π_Pno (WORKS_ON ⋈_Essn=Ssn (π_Ssn (σ_{Lname=‘Smith’}(EMPLOYEE))) ∪ π_Pno ((π_Dnumber (σ_{Lname=‘Smith’}(π_{Lname, Dnumber}(EMPLOYEE)))  _{Ssn=Mgr_ssn}DEPARTMENT)) ⋈_{Dnum-ber=Dnum}PROJECT)

Truy vấn 5. Liệt kê tên của tất cả nhân viên có từ hai người phụ thuộc trở lên.

Nói một cách chính xác, truy vấn này không thể thực hiện được trong đại số quan hệ (gốc) cơ bản. Chúng ta phải sử dụng phép toán TỔNG HỢP với hàm tổng hợp COUNT. Chúng tôi giả định rằng những người phụ thuộc của cùng một nhân viên có các giá trị Dependent_name riêng biệt.

T1(Ssn, No_of_dependents)← _Essn ℑ _{COUNT Dependent_name}(DEPENDENT)

T2 ← σ_{No_of_dependents>2}(T1)

RESULT ← π_{Lname, Fname}(T2 * EMPLOYEE)

Truy vấn 6. Truy xuất tên nhân viên không có người phụ thuộc.

Đây là một ví dụ về loại truy vấn sử dụng thao tác TRỪ (MINUS).

ALL_EMPS ← π_Ssn(EMPLOYEE)

EMPS_WITH_DEPS(Ssn) ← π_Essn(DEPENDENT)

EMPS_WITHOUT_DEPS ← (ALL_EMPS – EMPS_WITH_DEPS)

RESULT ← π_{Lname, Fname}(EMPS_WITHOUT_DEPS * EMPLOYEE)

Trước tiên, chúng tôi truy xuất mối quan hệ với tất cả Ssns của nhân viên trong ALL_EMPS. Sau đó, chúng tôi tạo một bảng có Ssns của những nhân viên có ít nhất một người phụ thuộc trong EMPS_WITH_DEPS. Sau đó, chúng tôi áp dụng thao tác MINUS để truy xuất Ssns của nhân viên mà không có người phụ thuộc trong EMPS_WITHOUT_DEPS và cuối cùng, tham gia hoạt động này với EMPLOYEE để truy xuất các thuộc tính mong muốn.Truy vấn có thể viết thành một dòng như sau:

π_{Lname, Fname}((π_Ssn(EMPLOYEE) – ρ_Ssn(π_Essn(DEPENDENT))) * EMPLOYEE)

Truy vấn 7. Liệt kê tên của những người quản lý có ít nhất một người phụ thuộc

MGRS(Ssn) ← π_{Mgr_ssn}(DEPARTMENT)

EMPS_WITH_DEPS(Ssn) ← π_Essn(DEPENDENT)

MGRS_WITH_DEPS ← (MGRS ∩ EMPS_WITH_DEPS)

RESULT ← π_{Lname, Fname}(MGRS_WITH_DEPS * EMPLOYEE)

Trong truy vấn này, chúng tôi truy xuất Ssns của người quản lý trong MGRS và Ssns của nhân viên có ít nhất một người phụ thuộc trong EMPS_WITH_DEPS, sau đó chúng tôi áp dụng thao tác SET INTERSECTION để lấy Ssns của người quản lý có ít nhất một người phụ thuộc

6. Phép tính quan hệ

Trong phần này và phần tiếp theo, chúng tôi giới thiệu một ngôn ngữ truy vấn chính thức khác cho mô hình quan hệ được gọi là phép tính quan hệ. Phần này giới thiệu ngôn ngữ được gọi là phép tính quan hệ bộ, và Phần 8.7 giới thiệu một biến thể gọi là phép tính quan hệ miền. Trong cả hai biến thể của phép tính quan hệ, chúng tôi viết một biểu thức khai báo để chỉ định yêu cầu truy xuất; do đó, không có mô tả về cách thức hoặc thứ tự đánh giá một truy vấn. Một biểu thức giải tích xác định những gì sẽ được truy xuất hơn là cách truy xuất nó. Do đó, phép tính quan hệ được coi là một ngôn ngữ phi thủ tục. Điều này khác với đại số quan hệ, nơi chúng ta phải viết một chuỗi các phép toán để chỉ định một yêu cầu truy xuất theo một thứ tự cụ thể của việc áp dụng các phép toán; do đó, nó có thể được coi là một cách thủ tục để nêu một truy vấn. Có thể lồng các phép toán đại số để tạo thành một biểu thức duy nhất; tuy nhiên, một thứ tự nhất định giữa các phép toán luôn được chỉ định rõ ràng trong một biểu thức đại số quan hệ. Thứ tự này cũng ảnh hưởng đến chiến lược đánh giá truy vấn. Một biểu thức tính toán có thể được viết theo nhiều cách khác nhau, nhưng cách nó được viết không liên quan đến cách đánh giá một truy vấn

Người ta đã chỉ ra rằng bất kỳ truy vấn nào có thể được chỉ định trong đại số quan hệ cơ bản cũng có thể được chỉ định trong phép tính quan hệ và ngược lại; nói cách khác, sức biểu đạt của các ngôn ngữ là đồng nhất. Điều này dẫn đến định nghĩa về khái niệm ngôn ngữ hoàn chỉnh về mặt quan hệ. Một ngôn ngữ truy vấn quan hệ L được coi là hoàn chỉnh về mặt quan hệ nếu chúng ta có thể biểu diễn trong L bất kỳ truy vấn nào có thể được biểu thị bằng phép tính quan hệ. Tính đầy đủ của quan hệ đã trở thành cơ sở quan trọng để so sánh sức mạnh biểu đạt của các ngôn ngữ truy vấn cấp cao. Tuy nhiên, như chúng ta đã thấy trong Phần 8.4, một số truy vấn thường xuyên được yêu cầu trong các ứng dụng cơ sở dữ liệu không thể được biểu diễn bằng phép tính hoặc đại số quan hệ cơ bản. Hầu hết các ngôn ngữ truy vấn quan hệ đều hoàn chỉnh về mặt quan hệ nhưng có khả năng biểu đạt cao hơn so với đại số quan hệ hoặc phép tính quan hệ do có các phép toán bổ sung như hàm tổng hợp, nhóm và sắp xếp thứ tự. Như chúng ta đã đề cập trong phần giới thiệu của chương này, phép tính quan hệ rất quan trọng vì hai lý do. Đầu tiên, nó có cơ sở vững chắc trong logic toán học. Thứ hai, ngôn ngữ truy vấn chuẩn (SQL) cho RDBMS có nền tảng cơ bản trong phép tính quan hệ bộ.

6.1 Biến tuple và quan hệ phạm vi

Phép tính quan hệ bộ dựa trên việc chỉ định số lượng biến bộ. Mỗi biến bộ thường dao động trên một quan hệ cơ sở dữ liệu cụ thể, nghĩa là biến đó có thể lấy giá trị của nó bất kỳ bộ nào từ quan hệ đó. Một truy vấn phép tính quan hệ bộ đơn giản có dạng:

{t | COND(t)}

trong đó t là một biến bộ và COND(t) là một biểu thức có điều kiện (Boolean) liên quan đến t đánh giá là TRUE hoặc FALSE đối với các phép gán khác nhau của các bộ cho biến t. Kết quả của một truy vấn như vậy là tập hợp tất cả các bộ t đánh giá COND(t) là TRUE. Các bộ này được cho là thỏa mãn COND(t). Ví dụ: để tìm tất cả nhân viên có mức lương trên 50.000 đô la, chúng ta có thể viết biểu thức tính toán bộ sau:

{t | EMPLOYEE(t) AND t.Salary>50000}

Điều kiện EMPLOYEE(t) xác định rằng quan hệ phạm vi của biến bộ t là EMPLOYEE. Mỗi bộ EMPLOYEE t thỏa mãn điều kiện t.Salary>50000 sẽ được truy xuất. Lưu ý rằng thuộc tính tham chiếu t.Salarylary của biến tuple t; ký hiệu này giống như cách các tên thuộc tính đủ điều kiện với tên quan hệ hoặc bí danh trong SQL, như chúng ta đã thấy trong Chương 6. Trong ký hiệu của Chương 5, t.Salary giống như cách viết t[Salary].

Truy vấn trước truy xuất tất cả các giá trị thuộc tính cho mỗi bộ EMPLOYEE được chọn. Để chỉ truy xuất một số thuộc tính—ví dụ, tên và họ—chúng tôi viết

t.Fname, t.Lname | EMPLOYEE(t) AND t.Salary>50000} Một cách không chính thức, chúng ta cần chỉ định thông tin sau trong biểu thức phép tính quan hệ bộ:

• Đối với mỗi biến bộ t, quan hệ phạm vi R của t. Giá trị này được xác định bởi một điều kiện có dạng R(t). Nếu chúng ta không chỉ định một quan hệ phạm vi, thì biến t sẽ có phạm vi trên tất cả các bộ có thể có “trong vũ trụ” vì nó không bị giới hạn trong bất kỳ một quan hệ nào.
• Một điều kiện để chọn các tổ hợp cụ thể của các bộ. Vì các biến bộ nằm trong phạm vi quan hệ phạm vi tương ứng của chúng, nên điều kiện được đánh giá cho mọi kết hợp có thể có của các bộ để xác định các kết hợp đã chọn mà điều kiện đánh giá là TRUE.
• Một tập hợp các thuộc tính được truy xuất, các thuộc tính được yêu cầu. Các giá trị của các thuộc tính này được truy xuất cho mỗi tổ hợp bộ dữ liệu đã chọn.

Trước khi chúng ta thảo luận về cú pháp chính thức của phép tính quan hệ bộ, hãy xem xét một truy vấn khác.

Truy vấn 0. Truy xuất ngày sinh và địa chỉ của nhân viên (hoặc các nhân viên) có tên là John B. Smith

Q0: {t.Bdate, t.Address | EMPLOYEE(t) AND t.Fname=‘John’ AND t.Minit=‘B’ AND t.Lname=‘Smith’}

Trong phép tính quan hệ bộ, trước tiên chúng tôi chỉ định các thuộc tính được yêu cầu t.Bdate và t.Address cho mỗi bộ t đã chọn. Sau đó, chúng tôi chỉ định điều kiện để chọn một bộ theo sau thanh (|)—cụ thể là, đó là một bộ của quan hệ EMPLOYEE có các giá trị thuộc tính Fname, Minit và Lname là 'John', 'B' và 'Smith', tương ứng.

6.2 Biểu thức và công thức trong phép tính quan hệ tuple

Biểu thức tổng quát của phép tính quan hệ bộ có dạng

{t1.Aj , t2.Ak, ... , tn.Am | COND(t1, t2, ..., tn, tn+1, tn+2, ..., tn+m)}

trong đó t1, t2, … , tn, tn+1, …, tn+m là các biến bộ, mỗi Ai là một thuộc tính của quan hệ mà ti nằm trên đó và COND là điều kiện hoặc công thức của phép tính quan hệ bộ. Một công thức được tạo thành từ các nguyên tử phép tính vị từ, có thể là một trong các cách sau:

• Một nguyên tử có dạng R(ti), trong đó R là tên quan hệ và ti là biến bộ. Nguyên tử này xác định phạm vi của biến bộ ti là quan hệ có tên là R. Nó đánh giá là TRUE nếu ti là một bộ trong quan hệ R và đánh giá là FALSE nếu không.
• Một nguyên tử có dạng ti.A op tj .B, trong đó op là một trong các toán tử so sánh trong tập {=, , ≥, ≠}, ti và tj là các biến bộ, A là một thuộc tính của quan hệ trên phạm vi ti nào và B là một thuộc tính của quan hệ mà tj phạm vi.
• Một nguyên tử có dạng ti.A op c hoặc c op tj .B, trong đó op là một trong các toán tử so sánh trong tập {=, , ≥, ≠}, ti và tj là các biến bộ, A là một thuộc tính của mối quan hệ mà ti nằm trong khoảng, B là một thuộc tính của mối quan hệ mà tj nằm trong khoảng và c là một giá trị không đổi.

Mỗi nguyên tử trước đánh giá TRUE hoặc FALSE cho một tổ hợp bộ dữ liệu cụ thể; đây được gọi là giá trị thực của một nguyên tử. Nói chung, một biến bộ t nằm trên tất cả các bộ có thể có trong vũ trụ. Đối với các nguyên tử có dạng R(t), nếu t được gán cho một bộ là thành viên của quan hệ R đã chỉ định, thì nguyên tử đó là TRUE; nếu không, nó là FALSE. Trong các nguyên tử loại 2 và 3, nếu các biến bộ được gán cho các bộ sao cho giá trị của các thuộc tính được chỉ định của các bộ thỏa mãn điều kiện, thì nguyên tử đó là TRUE.

Một công thức (điều kiện Boolean) được tạo thành từ một hoặc nhiều nguyên tử được kết nối thông qua các toán tử logic AND, OR và NOT và được định nghĩa đệ quy theo Quy tắc 1 và 2 như sau:

• Quy tắc 1: Mỗi nguyên tử là một công thức.
• Quy tắc 2: Nếu F1 và F2 là công thức, thì (F1 AND F2), (F1 OR F2), NOT (F1) và NOT (F2) cũng vậy. Giá trị thực của các công thức này được suy ra từ các công thức thành phần F1 và F2 của chúng như sau:
  • F1 AND F2 là TRUE nếu cả F1 và F2 đều TRUE ngược lại kết quả FALSE
  • F1 OR F2 là FALSE nếu cả F1 và F2 đều FALSE ngược lại kết quả là FALSE
  • NOT F1 là TRUE nếu F1 là FALSE và ngược lại
  • NOT F2 là TRUE nếu F2 là FALSE và ngược lại

6.3 Các bộ định lượng tồn tại và với mọi

Ngoài ra, hai ký hiệu đặc biệt được gọi là định lượng có thể xuất hiện trong công thức; đó là lượng từ với mọi (∀) và lượng từ tồn tại (∃). Giá trị thực cho các công thức có định lượng được mô tả trong Quy tắc 3 và 4 bên dưới; Tuy nhiên, trước tiên, chúng ta cần định nghĩa các khái niệm về các biến bộ tự do và bị ràng buộc trong một công thức. Một cách không chính thức, một biến bộ t bị ràng buộc nếu nó được lượng hóa, nghĩa là nó xuất hiện trong mệnh đề (∃t) hoặc (∀t); nếu không, nó là tự do. Chính thức, chúng tôi định nghĩa một biến bộ trong một công thức là tự do hoặc bị ràng buộc theo các quy tắc sau:

• Sự xuất hiện của một biến bộ trong công thức F là một nguyên tử tự do trong F
• Sự xuất hiện của một biến bộ t là tự do hoặc bị ràng buộc trong một công thức được tạo thành từ các liên kết logic—(F1 AND F2), (F1 OR F2), NOT(F1) và NOT(F2)— tùy thuộc vào việc nó là tự do hay ràng buộc ở F1 hoặc F2 (nếu nó xảy ra ở một trong hai). Lưu ý rằng trong một công thức có dạng F = (F1 AND F2) hoặc F = (F1 OR F2), một biến bộ có thể tự do trong F1 và bị ràng buộc trong F2 hoặc ngược lại; trong trường hợp này, một lần xuất hiện của biến bộ bị ràng buộc và lần xuất hiện khác là miễn phí trong F
• Tất cả các lần xuất hiện tự do của một biến bộ t trong F được liên kết trong một công thức F′ có dạng F′= (∃t (F) hoặc F′ = (∀t)(F). Biến bộ được liên kết với bộ định lượng được chỉ định trong F ′. Ví dụ, hãy xem xét các công thức sau:

F1: d.Dname = ‘Research’

F2: (∃t)(d.Dnumber = t.Dno)

F3: (∀d)(d.Mgr_ssn = ‘333445555’)

Biến bộ d là miễn phí trong cả F1 và F2, trong khi nó bị ràng buộc với bộ định lượng (∀) trong F3. Biến t được liên kết với bộ định lượng (∃) ở F2

Bây giờ chúng ta có thể đưa ra Quy tắc 3 và 4 cho định nghĩa của một công thức mà chúng ta đã bắt đầu trước đó:

• Quy tắc 3: Nếu F là một công thức thì (∃t)(F) cũng vậy, trong đó t là một biến bộ. Công thức (∃t)(F) là TRUE nếu công thức F đánh giá là TRUE đối với một số (ít nhất một) bộ được gán cho các lần xuất hiện tự do của t trong F; mặt khác, (∃t)(F) là FALSE
• Quy tắc 4: Nếu F là một công thức thì (∀t)(F) cũng vậy, trong đó t là một biến bộ. Công thức (∀t)(F) là TRUE nếu công thức F đánh giá là TRUE cho mọi bộ (trong vũ trụ) được gán cho các lần xuất hiện tự do của t trong F; mặt khác, (∀t)(F) là FALSE

Bộ định lượng (∃) được gọi là bộ định lượng tồn tại vì công thức (∃t)(F) là TRUE nếu tồn tại một số bộ làm cho F TRUE. Đối với bộ lượng hóa phổ quát, (∀t)(F) là TRUE nếu mọi bộ có thể được gán cho các lần xuất hiện tự do của t trong F được thay thế cho t và F là TRUE cho mọi sự thay thế như vậy. Nó được gọi là bộ định lượng phổ quát hoặc cho tất cả bởi vì mọi bộ trong vũ trụ các bộ phải làm cho F TRUE để biến công thức lượng hóa thành TRUE.

6.4 Truy vấn mẫu trong phép tính quan hệ Tuple

Chúng ta sẽ sử dụng một số truy vấn tương tự từ Phần 8.5 để hiểu rõ hơn cách các truy vấn tương tự được chỉ định trong đại số quan hệ và trong phép tính quan hệ. Lưu ý rằng một số truy vấn dễ xác định trong đại số quan hệ hơn là trong phép tính quan hệ và ngược lại.

Truy vấn 1. Truy xuất tên và địa chỉ của tất cả nhân viên làm việc cho bộ phận 'Research’

Q1: {t.Fname, t.Lname, t.Address | EMPLOYEE(t) AND (∃d)(DEPARTMENT(d) AND d.Dname=‘Research’ AND d.Dnumber=t.Dno)}

Các biến bộ miễn phí duy nhất trong một biểu thức tính toán quan hệ bộ phải là những biến xuất hiện ở bên trái của thanh (|). Trong Q1, t là biến tự do duy nhất; sau đó nó được liên kết liên tiếp với mỗi bộ dữ liệu. Nếu một bộ thỏa mãn các điều kiện được chỉ định sau thanh trong Q1, các thuộc tính Fname, Lname và Address được truy xuất cho mỗi bộ đó. Các điều kiện EMPLOYEE(t) và DEPARTMENT(d) xác định các quan hệ phạm vi cho t và d. Điều kiện d.Dname = 'Research' là điều kiện lựa chọn và tương ứng với thao tác CHỌN trong đại số quan hệ, trong khi điều kiện d.Dnumber = t.Dno là điều kiện nối và có mục đích tương tự như thao tác JOIN (INNER)

Truy vấn 2. Đối với mọi dự án đặt tại ‘Stafford’, hãy liệt kê số dự án, số bộ phận kiểm soát và họ, địa chỉ và ngày sinh của người quản lý bộ phận.

Q2: {p.Pnumber, p.Dnum, m.Lname, m.Bdate, m.Address | PROJECT(p) AND EMPLOYEE(m) AND p.Plocation=‘Stafford’ AND ((∃d)(DEPARTMENT(d) AND p.Dnum=d.Dnumber AND d.Mgr_ssn=m.Ssn))}

Trong Q2 có hai biến bộ tự do là p và m. Biến bộ d được liên kết với bộ lượng hóa tồn tại. Điều kiện truy vấn được đánh giá cho mọi tổ hợp các bộ được gán cho p và m, và trong số tất cả các tổ hợp có thể có của các bộ mà p và m bị ràng buộc, chỉ những tổ hợp thỏa mãn điều kiện mới được chọn.

Một số biến bộ trong một truy vấn có thể nằm trong cùng một mối quan hệ. Ví dụ: để chỉ định Q8—đối với mỗi nhân viên, truy xuất họ và tên của nhân viên cũng như họ và tên của người giám sát trực tiếp của anh ấy hoặc cô ấy—chúng ta chỉ định hai biến bộ e và s mà cả hai đều nằm trong quan hệ EMPLOYEE

Q8: {e.Fname, e.Lname, s.Fname, s.Lname | EMPLOYEE(e) AND EMPLOYEE(s) AND e.Super_ssn=s.Ssn}

Truy vấn 3. Tìm tên của các nhân viên làm việc trong tất cả các dự án do bộ phận số 5 kiểm soát.

Q0′: {e.Lname, e.Fname | EMPLOYEE(e) AND ((∃x)(∃w)(PROJECT(x) AND WORKS_ON(w) AND x.Dnum=5 AND w.Essn=e.Ssn AND x.Pnumber=w.Pno))}

Truy vấn 4. Lập danh sách số dự án cho các dự án liên quan đến một nhân viên có họ là 'Smith', với tư cách là công nhân hoặc quản lý của bộ phận kiểm soát dự án.

Q4: { p.Pnumber | PROJECT(p) AND (((∃e)(∃w)(EMPLOYEE(e) AND WORKS_ON(w) AND w.Pno=p.Pnumber AND e.Lname=‘Smith’ AND e.Ssn=w.Essn) ) OR ((∃m)(∃d)(EMPLOYEE(m) AND DEPARTMENT(d) AND p.Dnum=d.Dnumber AND d.Mgr_ssn=m.Ssn AND m.Lname=‘Smith’)))}

So sánh điều này với phiên bản đại số quan hệ của truy vấn này trong Phần 8.5. Phép toán UNION trong đại số quan hệ thường có thể được thay thế bằng phép nối OR trong phép toán quan hệ

6.5 Ký hiệu cho đồ thị truy vấn

Trong phần này, chúng tôi mô tả một ký hiệu đã được đề xuất để biểu diễn các truy vấn tính toán quan hệ không liên quan đến định lượng phức tạp ở dạng đồ họa. Các loại truy vấn này được gọi là truy vấn select-project-join vì chúng chỉ liên quan đến ba phép toán đại số quan hệ này. Ký hiệu có thể được mở rộng cho các truy vấn tổng quát hơn, nhưng chúng tôi không thảo luận về các phần mở rộng này ở đây. Biểu diễn đồ họa này của truy vấn được gọi là biểu đồ truy vấn. Hình 8.13 hiển thị biểu đồ truy vấn cho Q2. Các quan hệ trong truy vấn được biểu thị bằng các nút quan hệ, được hiển thị dưới dạng các vòng tròn đơn lẻ. Các giá trị không đổi, thường là từ các điều kiện lựa chọn truy vấn, được biểu thị bằng các nút không đổi, được hiển thị dưới dạng hình tròn hoặc hình bầu dục kép. Các điều kiện lựa chọn và join được thể hiện bằng các cạnh của đồ thị (các đường kết nối các nút), như trong Hình 8.13. Cuối cùng, các thuộc tính được truy xuất từ mỗi quan hệ được hiển thị trong ngoặc vuông phía trên mỗi quan hệ.

Biểu diễn đồ thị truy vấn không chỉ ra một thứ tự cụ thể để xác định hoạt động nào cần thực hiện trước và do đó là biểu diễn trung tính hơn của truy vấn select-project-join so với biểu diễn cây truy vấn, trong đó thứ tự thực hiện được quy định ngầm. Chỉ có một biểu đồ truy vấn duy nhất tương ứng với mỗi truy vấn. Mặc dù một số kỹ thuật tối ưu hóa truy vấn dựa trên biểu đồ truy vấn, nhưng hiện nay người ta thường chấp nhận rằng cây truy vấn được ưu tiên hơn vì trên thực tế, trình tối ưu hóa truy vấn cần hiển thị thứ tự các thao tác để thực hiện truy vấn, điều này không thể thực hiện được trong biểu đồ truy vấn.

Trong phần tiếp theo, chúng ta thảo luận về mối quan hệ giữa các bộ định lượng phổ quát và hiện sinh và chỉ ra cách cái này có thể được chuyển đổi thành cái kia.

6.6 Biến đổi các bộ lượng hóa với mọi và tồn tại

Bây giờ chúng tôi giới thiệu một số phép biến đổi nổi tiếng từ logic toán học liên quan đến các lượng hóa phổ quát và tồn tại. Có thể biến đổi một lượng từ phổ quát thành một lượng từ tồn tại, và ngược lại, để có được một biểu thức tương đương. Một phép biến đổi tổng quát có thể được mô tả một cách không chính thức như sau: Chuyển dạng một loại lượng từ này sang dạng khác với phủ định (đứng trước NOT); AND và OR thay thế cho nhau; một công thức phủ định trở thành không phủ định; và một công thức không phủ định trở thành phủ định. Có thể nêu một số trường hợp đặc biệt của phép biến đổi này như sau, trong đó ký hiệu ≡ là viết tắt của:

(∀x) (P(x)) ≡ NOT (∃x) (NOT (P(x)))

(∃x) (P(x)) ≡ NOT (∀x) (NOT (P(x)))

(∀x) (P(x) AND Q(x)) ≡ NOT (∃x) (NOT (P(x)) OR NOT (Q(x)))

(∀x) (P(x) OR Q(x)) ≡ NOT (∃x) (NOT (P(x)) AND NOT (Q(x)))

(∃x) (P(x)) OR Q(x)) ≡ NOT (∀x) (NOT (P(x)) AND NOT (Q(x)))

(∃x) (P(x) AND Q(x)) ≡ NOT (∀x) (NOT (P(x)) OR NOT (Q(x)))

Cũng lưu ý rằng điều sau đây là TRUE, trong đó ký hiệu ⇒ là viết tắt của ngụ ý:

(∀x)(P(x)) ⇒ (∃x)(P(x))

NOT (∃x)(P(x)) ⇒ NOT (∀x)(P(x))

6.7 Sử dụng Universal Quantifier trong truy vấn

Bất cứ khi nào chúng ta sử dụng một bộ định lượng phổ quát, sẽ rất tốt khi tuân theo một số quy tắc để đảm bảo rằng biểu thức của chúng ta có ý nghĩa. Chúng ta thảo luận các quy tắc này đối với truy vấn Q3.

Truy vấn 3. Liệt kê tên của các nhân viên làm việc trong tất cả các dự án được kiểm soát bởi bộ phận số 5. Một cách để xác định truy vấn này là sử dụng lượng từ chung như minh họa:

Q3: {e.Lname, e.Fname | EMPLOYEE(e) AND ((∀x)(NOT(PROJECT(x)) OR NOT (x.Dnum=5) OR ((∃w)(WORKS_ON(w) AND w.Essn=e.Ssn AND x.Pnumber=w.Pno))))}

Chúng ta có thể chia Q3 thành các thành phần cơ bản như sau:

Q3: {e.Lname, e.Fname | EMPLOYEE(e) AND F′}

F′ = ((∀x)(NOT(PROJECT(x)) OR F1))

F1 = NOT(x.Dnum=5) OR F2

F2 = ((∃w)(WORKS_ON(w) AND w.Essn=e.Ssn AND x.Pnumber=w.Pno))

Chúng tôi muốn đảm bảo rằng một nhân viên được chọn e làm việc trên tất cả các dự án do bộ phận 5 kiểm soát, nhưng định nghĩa của bộ lượng hóa phổ quát nói rằng để làm cho công thức lượng hóa TRUE, công thức bên trong phải TRUE cho tất cả các bộ. Bí quyết là loại trừ khỏi phép định lượng phổ quát tất cả các bộ dữ liệu mà chúng ta không quan tâm bằng cách đặt điều kiện là TRUE cho tất cả các bộ dữ liệu đó. Điều này là cần thiết bởi vì một biến bộ dữ liệu được định lượng phổ biến, chẳng hạn như x trong Q3, phải đánh giá là TRUE cho mọi bộ dữ liệu có thể được gán cho nó để làm cho công thức định lượng là TRUE.

Các bộ đầu tiên cần loại trừ (bằng cách làm cho chúng tự động đánh giá thành TRUE) là những bộ không thuộc quan hệ R quan tâm. Trong Q3, việc sử dụng biểu thức NOT(PROJECT(x)) bên trong công thức định lượng phổ biến sẽ đánh giá TRUE tất cả các bộ x không nằm trong quan hệ PROJECT. Sau đó, chúng tôi loại trừ các bộ mà chúng tôi không quan tâm khỏi chính R. Trong Q3, sử dụng biểu thức NOT(x.Dnum=5) đánh giá là TRUE tất cả các bộ x nằm trong quan hệ PROJECT nhưng không được kiểm soát bởi bộ phận 5. Cuối cùng, chúng tôi chỉ định một điều kiện F2 phải giữ cho tất cả các bộ còn lại trong R. Do đó, chúng ta có thể giải thích Q3 như sau:

• Để công thức F′ = (∀x)(F) là TRUE, chúng ta phải có công thức F là ĐÚNG cho tất cả các bộ trong vũ trụ có thể được gán cho x. Tuy nhiên, trong Q3, chúng ta chỉ quan tâm đến việc F là TRUE đối với tất cả các bộ của quan hệ DỰ ÁN được kiểm soát bởi bộ phận 5. Do đó, công thức F có dạng (NOT(PROJECT(x)) OR F1). Điều kiện 'NOT (PROJECT(x)) OR …' là ĐÚNG đối với tất cả các bộ dữ liệu không có trong quan hệ DỰ ÁN và có tác dụng loại bỏ các bộ dữ liệu này khỏi việc xem xét giá trị thực của F1. Đối với mỗi bộ trong quan hệ DỰ ÁN, F1 phải là TRUE nếu F′ là TRUE.
• Sử dụng cùng một dòng lập luận, chúng tôi không muốn xem xét các bộ trong quan hệ PROJECT không được kiểm soát bởi bộ phận số 5, vì chúng tôi chỉ quan tâm đến các bộ PROJECT có Dnum=5. Do đó, chúng ta có thể viết:

IF (x.Dnum=5) THEN F2 tương đương (NOT (x.Dnum=5) OR F2)

• Do đó, công thức F1 có dạng NOT(x.Dnum=5) OR F2. Trong ngữ cảnh của Q3, điều này có nghĩa là, đối với một bộ x trong quan hệ PROJECT, Dnum≠5 của nó hoặc nó phải thỏa mãn F2.
• Cuối cùng, F2 đưa ra điều kiện mà chúng tôi muốn giữ cho một bộ EMPLOYEE đã chọn: nhân viên đó làm việc trên mọi bộ PROJECT chưa được loại trừ. Các bộ dữ liệu nhân viên như vậy được chọn bởi truy vấn.

Trong tiếng Anh, Q3 đưa ra điều kiện sau để chọn một bộ EMPLOYEE e: Đối với mọi bộ x trong quan hệ PROJECT với x.Dnum=5, phải tồn tại một bộ w trong WORKS_ON sao cho w.Essn=e.Ssn và w. Pno=x.Pnumber. Điều này tương đương với việc nói rằng EMPLOYEE e làm việc trên mọi PROJECT x trong DEPARTMENT số 5. (Chà!)

Bằng cách sử dụng phép chuyển đổi chung từ lượng từ phổ biến sang lượng từ tồn tại được đưa ra trong Phần 6.6, chúng ta có thể diễn đạt lại truy vấn trong Q3 như được trình bày trong Q3A, sử dụng lượng từ tồn tại phủ định thay vì lượng từ phổ quát:

Q3A: {e.Lname, e.Fname | EMPLOYEE(e) AND (NOT (∃x) (PROJECT(x) AND (x.Dnum=5) and (NOT (∃w)(WORKS_ON(w) AND w.Essn=e.Ssn AND x.Pnumber=w.Pno))))}

Bây giờ chúng tôi đưa ra một số ví dụ bổ sung về các truy vấn sử dụng bộ định lượng.

Truy vấn 6. Liệt kê tên nhân viên không có người phụ thuộc.

Q6: {e.Fname, e.Lname | EMPLOYEE(e) AND (NOT (∃d)(DEPENDENT(d) AND e.Ssn=d.Essn))}

Sử dụng quy tắc biến đổi tổng quát, chúng ta có thể viết lại Q6 như sau:

Q6A: {e.Fname, e.Lname | EMPLOYEE(e) AND ((∀d)(NOT(DEPENDENT(d)) OR NOT(e.Ssn=d.Essn)))}

Truy vấn 7. Liệt kê tên của những người quản lý có ít nhất một người phụ thuộc.

Q7: {e.Fname, e.Lname | EMPLOYEE(e) AND ((∃d)(∃ρ)(DEPARTMENT(d) AND DEPENDENT(ρ) AND e.Ssn=d.Mgr_ssn AND ρ.Essn=e.Ssn))}

Truy vấn này được xử lý bằng cách diễn giải những người quản lý có ít nhất một người phụ thuộc thành những người quản lý có một số người phụ thuộc.

6.8 Biểu thức an toàn

Bất cứ khi nào chúng ta sử dụng các lượng từ phổ quát, lượng từ tồn tại hoặc phủ định của các vị từ trong một biểu thức tính toán, chúng ta phải đảm bảo rằng biểu thức thu được có nghĩa. Một biểu thức an toàn trong phép tính quan hệ là một biểu thức đảm bảo cho kết quả là một số hữu hạn các bộ; mặt khác, biểu thức được gọi là không an toàn. Ví dụ, biểu thức

{t | NOT (EMPLOYEE(t))}

không an toàn vì nó tạo ra tất cả các bộ dữ liệu không phải là bộ dữ liệu EMPLOYEE, có số lượng vô hạn. Nếu chúng ta tuân theo các quy tắc cho Q3 đã thảo luận trước đó, chúng ta sẽ nhận được một biểu thức an toàn khi sử dụng các bộ lượng hóa phổ quát. Chúng ta có thể định nghĩa các biểu thức an toàn chính xác hơn bằng cách đưa ra khái niệm miền của biểu thức phép tính quan hệ bộ: Đây là tập hợp tất cả các giá trị xuất hiện dưới dạng các giá trị không đổi trong biểu thức hoặc tồn tại trong bất kỳ bộ nào trong các quan hệ được tham chiếu trong biểu thức. Ví dụ, miền của {t | NOT(EMPLOYEE(t))} là tập hợp tất cả các giá trị thuộc tính xuất hiện trong một số bộ của quan hệ EMPLOYEE (đối với bất kỳ thuộc tính nào). Miền của biểu thức Q3A sẽ bao gồm tất cả các giá trị xuất hiện trong EMPLOYEE, PROJECT và WORKS_ON (kết hợp với giá trị 5 xuất hiện trong chính truy vấn đó)

Một biểu thức được cho là an toàn nếu tất cả các giá trị trong kết quả của nó đều thuộc miền của biểu thức. Lưu ý rằng kết quả của {t | NOT(EMPLOYEE(t))} là không an toàn, vì nói chung, nó sẽ bao gồm các bộ (và do đó là các giá trị) từ bên ngoài quan hệ EMPLOYEE; các giá trị đó không nằm trong miền của biểu thức. Tất cả các ví dụ khác của chúng tôi là biểu thức an toàn

7. Phép tính quan hệ miền

Có một loại phép tính quan hệ khác được gọi là phép tính quan hệ miền, hay đơn giản là phép tính miền. Về mặt lịch sử, trong khi SQL (xem Chương 6 và 7), dựa trên phép tính quan hệ bộ, được phát triển bởi IBM Research tại San Jose, California, thì một ngôn ngữ khác gọi là QBE (Truy vấn theo ví dụ), có liên quan đến phép tính miền. , được phát triển gần như đồng thời tại Trung tâm nghiên cứu IBM T. J. Watson ở Yorktown Heights, New York. Đặc tả chính thức của phép tính miền đã được đề xuất sau khi phát triển ngôn ngữ và hệ thống QBE.

Phép tính miền khác với phép tính bộ ở loại biến được sử dụng trong công thức: Thay vì có các biến có phạm vi trên các bộ, các biến có phạm vi trên các giá trị đơn lẻ từ các miền thuộc tính. Để hình thành mối quan hệ bậc n cho một kết quả truy vấn, chúng ta phải có n biến miền này—một biến cho mỗi thuộc tính. Biểu thức của phép tính miền có dạng

{x1, x2, ..., xn | COND(x1, x2, ..., xn, xn+1, xn+2, ..., xn+m)}

trong đó x1, x2, … , xn, xn+1, xn+2, … , xn+m là các biến miền có phạm vi trên các miền (của thuộc tính) và COND là điều kiện hoặc công thức của phép tính quan hệ miền.

Một công thức được tạo thành từ các nguyên tử. Nguyên tử của một công thức hơi khác so với nguyên tử của phép tính bộ và có thể là một trong các nguyên tử sau:

• Một nguyên tử có dạng R(x1, x2, … , xj ), trong đó R là tên của một quan hệ bậc j và mỗi xi, 1 ≤ i ≤ j, là một biến miền. Nguyên tử này nói rằng một danh sách các giá trị của phải là một bộ trong quan hệ có tên là R, trong đó xi là giá trị của giá trị thuộc tính thứ i của bộ. Để làm cho biểu thức tính toán miền ngắn gọn hơn, chúng ta có thể bỏ dấu phẩy trong danh sách các biến; do đó, chúng ta có thể viết:

{x1, x2, ..., xn | R(x1 x2 x3) AND ...} thay vì {x1, x2, ... , xn | R(x1, x2, x3) AND ...}

• Một nguyên tử có dạng xi op xj, trong đó op là một trong các toán tử so sánh trong tập {=, <, ≤, >, ≥, ≠}, và xi và xj là các biến miền.
• Một nguyên tử có dạng xi op c hoặc c op xj , trong đó op là một trong các toán tử so sánh trong tập {=, , ≥, ≠}, xi và xj là các biến miền và c là một giá trị không đổi.

Như trong phép tính bộ, các nguyên tử đánh giá là TRUE hoặc FALSE cho một tập hợp các giá trị cụ thể, được gọi là giá trị thực của các nguyên tử. Trong trường hợp 1, nếu các biến miền được gán các giá trị tương ứng với một bộ của quan hệ R đã chỉ định, thì nguyên tử là TRUE. Trong trường hợp 2 và 3, nếu các biến miền được gán giá trị thỏa mãn điều kiện, thì nguyên tử là TRUE.

Theo cách tương tự với phép tính quan hệ bộ, các công thức được tạo thành từ các nguyên tử, biến và đại lượng, vì vậy chúng tôi sẽ không nhắc lại các đặc điểm kỹ thuật cho các công thức ở đây. Dưới đây là một số ví dụ về các truy vấn được chỉ định trong phép tính miền. Chúng ta sẽ sử dụng các chữ cái viết thường l, m, n, … , x, y, z cho các biến miền.

Truy vấn 0. Liệt kê ngày sinh và địa chỉ của nhân viên có tên là ‘John B. Smith’.

Q0: {u, v | (∃q) (∃r) (∃s) (∃t) (∃w) (∃x) (∃y) (∃z) (EMPLOYEE(qrstuvwxyz) AND q=‘John’ AND r=‘B’ AND s=‘Smith’)}

Chúng ta cần mười biến cho quan hệ EMPLOYEE, một biến nằm trong từng miền thuộc tính của EMPLOYEE theo thứ tự. Trong số mười biến q, r, s, …, z, chỉ có u và v là miễn phí, bởi vì chúng xuất hiện ở bên trái của thanh và do đó không bị ràng buộc với một bộ định lượng. Trước tiên, chúng tôi chỉ định các thuộc tính được yêu cầu, Bdate và Address, bằng các biến miền miễn phí u cho BDATE và v cho ADDRESS. Sau đó, chúng tôi chỉ định điều kiện để chọn một bộ theo sau thanh (|)—cụ thể là chuỗi các giá trị được gán cho các biến qrstuvwxyz là một bộ của quan hệ EMPLOYEE và rằng các giá trị cho q (Tên), r (Minit), và s (Lname) tương ứng là 'John', 'B' và 'Smith'. Để thuận tiện, chúng tôi sẽ chỉ định lượng những biến thực sự xuất hiện trong một điều kiện (đây sẽ là q, r và s trong Q0) trong phần còn lại của các ví dụ của chúng tôi

Một ký hiệu tốc ký thay thế, được sử dụng trong QBE, để viết truy vấn này là gán trực tiếp các hằng số 'John', 'B' và 'Smith' như được hiển thị trong Q0A. Ở đây, tất cả các biến không xuất hiện ở bên trái của thanh đều được định lượng tồn tại hoàn toàn:

Q0A: {u, v | EMPLOYEE(‘John’, ‘B’, ‘Smith’, t, u, v, w, x, y, z)}

Truy vấn 1. Truy xuất tên và địa chỉ của tất cả nhân viên làm việc cho bộ phận 'Research’.

Q1: {q, s, v | (∃z) (∃l) (∃m) (EMPLOYEE(qrstuvwxyz) AND DEPARTMENT(lmno) AND l=‘Research’ AND m=z)}

Một điều kiện liên quan đến hai biến miền bao gồm các thuộc tính từ hai mối quan hệ, chẳng hạn như m = z trong Q1, là một điều kiện nối, trong khi một điều kiện liên quan đến một biến miền với một hằng số, chẳng hạn như l = 'Research', là một điều kiện điều kiện lựa chọn.

Truy vấn 2. Đối với mọi dự án đặt tại ‘Stafford’, hãy liệt kê số dự án, số bộ phận kiểm soát và họ, địa chỉ và ngày sinh của người quản lý bộ phận.

Q2: {i, k, s, u, v | (∃j)(∃m)(∃n)(∃t)(PROJECT(hijk) AND EMPLOYEE(qrstuvwxyz) AND DEPARTMENT(lmno) AND k=m AND n=t AND j=‘Stafford’)}

Truy vấn 6. Truy xuất tên nhân viên không có người phụ thuộc.

Q6: {q, s | (∃t)(EMPLOYEE(qrstuvwxyz) AND (NOT(∃l)(DEPENDENT(lmnop) AND t=l)))}

Q6 có thể được trình bày lại bằng cách sử dụng các lượng từ chung thay vì các lượng từ tồn tại, như trong Q6A:

Q6A: {q, s | (∃t)(EMPLOYEE(qrstuvwxyz) AND ((∀l)(NOT(DEPENDENT(lmnop)) OR NOT(t=l))))}

Truy vấn 7. Liệt kê tên của những người quản lý có ít nhất một người phụ thuộc

Q7: {s, q | (∃t)(∃j)(∃l)(EMPLOYEE(qrstuvwxyz) AND DEPARTMENT(hijk) AND DEPENDENT(lmnop) AND t=j AND l=t)}

Như chúng tôi đã đề cập trước đó, có thể chỉ ra rằng bất kỳ truy vấn nào có thể được biểu thị bằng đại số quan hệ cơ bản cũng có thể được biểu thị bằng phép tính quan hệ miền hoặc bộ. Ngoài ra, bất kỳ biểu thức an toàn nào trong miền hoặc phép tính quan hệ bộ có thể được biểu diễn trong đại số quan hệ cơ bản.

Ngôn ngữ QBE dựa trên phép tính quan hệ miền, mặc dù điều này đã được nhận ra sau đó, sau khi phép tính miền được chính thức hóa. QBE là một trong những ngôn ngữ truy vấn đồ họa đầu tiên với cú pháp tối thiểu được phát triển cho các hệ thống cơ sở dữ liệu. Nó được phát triển tại IBM Research và có sẵn dưới dạng một sản phẩm thương mại của IBM như một phần của tùy chọn giao diện Cơ sở quản lý truy vấn (QMF) cho DB2. Những ý tưởng cơ bản được sử dụng trong QBE đã được áp dụng trong một số sản phẩm thương mại khác.

8. Tóm tắt

• Tập hợp các phép toán cơ bản (phép chọn - Select, phép chiếu - Project, ....) cho mô hình quan hệ được gọi là đại số quan hệ. Các phép toán này cho phép người dùng đưa ra các yêu cầu truy vấn cơ bản. Kết quả của truy vấn là một quan hệ mới có thể được hình thành từ một hoặc nhiều quan hệ. Một chuỗi các phép toán đại số quan hệ tạo nên biểu thức đại số quan hệ (relational algebra expression), kết quả của nó cũng là một quan hệ thể hiện kết quả truy vấn dữ liệu trong CSDL
• Tập hợp các phép toán bao gồm:​​​​​​​

1. Chọn (select)
2. Chiếu (project)
3. Hội (union)
4. Hiệu (difference -)
5. Tích Decartes (cartesian product X) => được gọi là tập đầy đủ (complete set), vì mọi biểu thức đại số quan hệ khác đều có thể biểu diễn bằng cách kết hợp từ 5 phép toán này​​​​​​​

• Phép toán quan hệ là ngôn ngữ truy vấn hình thức, tương đương với đại số quan hệ. Một biểu thức của phép toán quan hệ (expression) sẽ tạo ra một quan hệ mới, nó được đặc tả qua thuật ngữ biến (variables) trãi trên các hàng (trong tuple calculus) hoặc trên các cột (trong domain calculus). Trong biểu thức tính toán, không có trình tự các phép toán để chỉ ra cách lấy kết quả (how), mà nó chỉ đặc tả thông tin gì cần lấy ra (what). Đây là đặc điểm phân biệt giữa đại số quan hệ và phép toán quan hệ